函数 的图象与 轴交于点 ,顶点坐标为 ,其中 .以下结论正确的是
① ;
②函数 在 和 处的函数值相等;
③函数 的图象与 的函数图象总有两个不同交点;
④函数 在 内既有最大值又有最小值.
A.①③B.①②③C.①④D.②③④
阅读以下材料,并解决相应问题:
小明在课外学习时遇到这样一个问题:
定义:如果二次函数 , 、 、 是常数)与 , 、 、 是常数)满足 , , ,则这两个函数互为“旋转函数”.求函数 的旋转函数,小明是这样思考的,由函数 可知, , , ,根据 , , ,求出 , , 就能确定这个函数的旋转函数.
请思考小明的方法解决下面问题:
(1)写出函数 的旋转函数.
(2)若函数 与 互为旋转函数,求 的值.
(3)已知函数 的图象与 轴交于 、 两点,与 轴交于点 ,点 、 、 关于原点的对称点分别是 、 、 ,试求证:经过点 、 、 的二次函数与 互为“旋转函数”.
规定:如果关于 的一元二次方程 有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”.现有下列结论:
①方程 是倍根方程;
②若关于 的方程 是倍根方程,则 ;
③若关于 的方程 是倍根方程,则抛物线 与 轴的公共点的坐标是 和 ;
④若点 在反比例函数 的图象上,则关于 的方程 是倍根方程.
上述结论中正确的有
A.①②B.③④C.②③D.②④
已知正方形 中 、 、 、 ,有一抛物线 向下平移 个单位 与正方形 的边(包括四个顶点)有交点,则 的取值范围是 .
如图,抛物线 与 轴交于点 ,对称轴为直线 ,平行于 轴的直线与抛物线交于 、 两点,点 在对称轴左侧, .
(1)求此抛物线的解析式.
(2)点 在 轴上,直线 将 面积分成 两部分,请直接写出 点坐标.
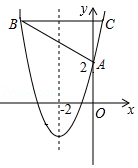
在平面直角坐标系内,已知点 ,点 都在直线 上,若抛物线 与线段 有两个不同的交点,则 的取值范围是

A. B.
B.C. 或 D.
如图,抛物线 与 轴交于 , 两点,与 轴交于点 ,顶点为 ,以 为直径作 .下列结论:①抛物线的对称轴是直线 ;② 的面积为 ;③抛物线上存在点 ,使四边形 为平行四边形;④直线 与 相切.其中正确结论的个数是

A.1B.2C.3D.4
已知函数 是常数, ,下列结论正确的是
A.当 时,函数图象经过点
B.当 时,函数图象与 轴没有交点
C.若 ,函数图象的顶点始终在 轴的下方
D.若 ,则当 时, 随 的增大而增大
在平面直角坐标系中,二次函数 的图象如图所示,点 , , , 是该二次函数图象上的两点,其中 ,则下列结论正确的是

A. B.
C. 的最小值是 D. 的最小值是
将抛物线 向左平移2个单位长度得到的抛物线经过三点 , , , ,则 , , 的大小关系是
A. B.
C. D.
如图,抛物线 与 轴交于点 ,点 的坐标为 ,在第四象限抛物线上有一点 ,若 是以 为底边的等腰三角形,则点 的横坐标为

A. B. C. D. 或
试题篮
()