如图, 在平面直角坐标系中, 点 ,在
,在 轴上任取一点
轴上任取一点 ,完成以下作图步骤:
,完成以下作图步骤:
①连接 . 作线段
. 作线段 的垂直平分线
的垂直平分线 ,过点
,过点 作
作 轴的垂线
轴的垂线 ,记
,记 ,
, 的交点为
的交点为 ;
;
②在 轴上多次改变点
轴上多次改变点 的位置, 用①的方法得到相应的点
的位置, 用①的方法得到相应的点 ,把这些点用平滑的曲线顺次连接起来, 得到的曲线是
,把这些点用平滑的曲线顺次连接起来, 得到的曲线是


A . 直线B . 抛物线C . 双曲线D . 双曲线的一支
如图, 在平面直角坐标系中, 点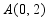 ,在
,在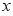 轴上任取一点
轴上任取一点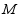 ,完成以下作图步骤:
,完成以下作图步骤:
①连接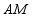 . 作线段
. 作线段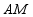 的垂直平分线
的垂直平分线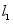 ,过点
,过点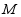 作
作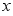 轴的垂线
轴的垂线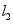 ,记
,记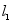 ,
,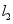 的交点为
的交点为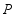 ;
;
②在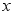 轴上多次改变点
轴上多次改变点 的位置, 用①的方法得到相应的点
的位置, 用①的方法得到相应的点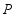 ,把这些点用平滑的曲线顺次连接起来, 得到的曲线是
,把这些点用平滑的曲线顺次连接起来, 得到的曲线是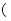
A . 直线B . 抛物线C . 双曲线D . 双曲线的一支
二次函数 ,若 , ,点 , , , 在该二次函数的图象上,其中 , ,则
| A. |
|
B. |
|
| C. |
|
D. |
、 的大小无法确定 |
对于一个函数,自变量 取 时,函数值 等于0,则称 为这个函数的零点.若关于 的二次函数 有两个不相等的零点 , ,关于 的方程 有两个不相等的非零实数根 , ,则下列关系式一定正确的是
| A. |
|
B. |
|
C. |
|
D. |
|
在平面直角坐标系 中,对于横、纵坐标相等的点称为"好点".下列函数的图象中不存在"好点"的是
| A. |
|
B. |
|
C. |
|
D. |
|
若抛物线 经过第四象限的点 ,则关于 的方程 的根的情况是
| A. |
有两个大于1的不相等实数根 |
| B. |
有两个小于1的不相等实数根 |
| C. |
有一个大于1另一个小于1的实数根 |
| D. |
没有实数根 |
若二次函数 的图象,过不同的六点 、 、 、 , 、 、 ,则 、 、 的大小关系是
| A. |
|
B. |
|
C. |
|
D. |
|
如图是二次函数 图象的一部分,对称轴为 ,且经过点 .下列说法:
① ;② ;③ ;④若 , , , 是抛物线上的两点,则 ;⑤ (其中 .
其中说法正确的是

| A. |
①②④⑤ |
B. |
①②④ |
C. |
①④⑤ |
D. |
③④⑤ |
抛物线 的对称轴是直线 ,且过点 .顶点位于第二象限,其部分图象如图所示,给出以下判断:
① 且 ;
② ;
③ ;
④ ;
⑤直线 与抛物线 两个交点的横坐标分别为 , ,则 .
其中正确的个数有

| A. |
5个 |
B. |
4个 |
C. |
3个 |
D. |
2个 |
已知二次函数 的图象如图所示,下列结论:① ,② ,③ ,④ ,正确的是

| A. |
①② |
B. |
①④ |
C. |
②③ |
D. |
②④ |
二次函数 的图象如图所示,下列结论中正确的是
①
②
③
④

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
已知二次函数 的 与 的部分对应值如表:
|
|
|
0 |
2 |
3 |
4 |
|
|
5 |
0 |
|
|
0 |
下列结论:①抛物线的开口向上;②抛物线的对称轴为直线 ;③当 时, ;④抛物线与 轴的两个交点间的距离是4;⑤若 , , , 是抛物线上两点,则 ,其中正确的个数是
| A. |
2 |
B. |
3 |
C. |
4 |
D. |
5 |
二次函数 的部分图象如图所示,图象过点 ,对称轴为直线 ,下列结论:
① ② ③ ④当 时,
其中正确的结论有

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
二次函数 , , 是常数, 的自变量 与函数值 的部分对应值如下表:
|
|
|
|
|
0 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
且当 时,与其对应的函数值 .有下列结论:
① ;② 和3是关于 的方程 的两个根;③ .
其中,正确结论的个数是
| A. |
0 |
B. |
1 |
C. |
2 |
D. |
3 |
试题篮
()