将一个直角三角形纸片 放置在平面直角坐标系中,点 ,点 ,点 在第一象限, , ,点 在边 上(点 不与点 , 重合).
(Ⅰ)如图①,当 时,求点 的坐标;
(Ⅱ)折叠该纸片,使折痕所在的直线经过点 ,并与 轴的正半轴相交于点 ,且 ,点 的对应点为 ,设 .
①如图②,若折叠后△ 与 重叠部分为四边形, , 分别与边 相交于点 , ,试用含有 的式子表示 的长,并直接写出 的取值范围;
②若折叠后△ 与 重叠部分的面积为 ,当 时,求 的取值范围(直接写出结果即可).

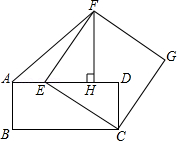
如图,在矩形 中, ,点 在边 上,连接 ,以 为边向右上方作正方形 ,作 ,垂足为 ,连接 .
(1)求证: ;
(2)当 为何值时, 的面积最大?
如图1,在平面直角坐标系中,直线 分别与 轴、 轴交于点 , , ,等边 的顶点 与原点 重合, 边落在 轴正半轴上,点 恰好落在线段 上,将等边 从图1的位置沿 轴正方向以每秒1个单位长度的速度平移,边 , 分别与线段 交于点 , (如图2所示),设 平移的时间为 .
(1)等边 的边长为 ;
(2)在运动过程中,当 时, 垂直平分 ;
(3)若在 开始平移的同时.点 从 的顶点 出发.以每秒2个单位长度的速度沿折线 运动.当点 运动到 时即停止运动. 也随之停止平移.
①当点 在线段 上运动时,若 与 相似.求 的值;
②当点 在线段 上运动时,设 ,求 与 的函数关系式,并求出 的最大值及此时点 的坐标.

设 、 是任意两个实数,用 , 表示 、 两数中较大者,例如: , , , , , ,参照上面的材料,解答下列问题:
(1) , , , ;
(2)若 , ,求 的取值范围;
(3)求函数 与 的图象的交点坐标,函数 的图象如图所示,请你在图中作出函数 的图象,并根据图象直接写出 , 的最小值.

如图,在正方形中,
,
为对角线
上一动点,连接
,
,过
点作
,交直线
于点
.
点从
点出发,沿着
方向以每秒
的速度运动,当点
与点
重合时,运动停止.设
的面积为
,
点的运动时间为
秒.

(1)求证:;
(2)求与
之间关系的函数表达式,并写出自变量
的取值范围;
(3)求面积的最大值.
设二次函数,
是实数).
(1)甲求得当时,
;当
时,
;乙求得当
时,
.若甲求得的结果都正确,你认为乙求得的结果正确吗?说明理由.
(2)写出二次函数图象的对称轴,并求该函数的最小值(用含,
的代数式表示).
(3)已知二次函数的图象经过和
两点
,
是实数),当
时,求证:
.
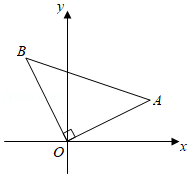
如图所示,在平面直角坐标系中, 为坐标原点,且 是等腰直角三角形, ,点 .
(1)求点 的坐标;
(2)求经过 、 、 三点的抛物线的函数表达式;
(3)在(2)所求的抛物线上,是否存在一点 ,使四边形 的面积最大?若存在,求出点 的坐标;若不存在,请说明理由.
如图,二次函数的图象经过点
与
.
(1)求,
的值;
(2)点是该二次函数图象上
,
两点之间的一动点,横坐标为
,写出四边形
的面积
关于点
的横坐标
的函数表达式,并求
的最大值.

(年新疆乌鲁木齐市)抛物线 与x轴交于A,B两点(OA<OB),与y轴交于点C.
与x轴交于A,B两点(OA<OB),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)点P从点O出发,以每秒2个单位长度的速度向点B运动,同时点E也从点O出发,以每秒1个单位长度的速度向点C运动,设点P的运动时间为t秒(0<t<2).
①过点E作x轴的平行线,与BC相交于点D(如图所示),当t为何值时, 的值最小,求出这个最小值并写出此时点E,P的坐标;
的值最小,求出这个最小值并写出此时点E,P的坐标;
②在满足①的条件下,抛物线的对称轴上是否存在点F,使△EFP为直角三角形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
(年贵州省黔南州)为了解都匀市交通拥堵情况,经统计分析,都匀彩虹桥上的车流速度v(千米/时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/时;当车流密度为20辆/千米时,车流速度为80千米/时.研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数.
(1)求彩虹桥上车流密度为100辆/千米时的车流速度;
(2)在交通高峰时段,为使彩虹桥上车流速度大于40千米/时且小于60千米/时,应控制彩虹桥上的车流密度在什么范围内?
(3)当车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.当20≤x≤220时,求彩虹桥上车流量y的最大值.
试题篮
()