如图,用绳子围成周长为 的矩形,记矩形的一边长为 ,它的邻边长为 ,矩形的面积为 .当 在一定范围内变化时, 和 都随 的变化而变化,则 与 , 与 满足的函数关系分别是

| A. |
一次函数关系,二次函数关系 |
| B. |
反比例函数关系,二次函数关系 |
| C. |
一次函数关系,反比例函数关系 |
| D. |
反比例函数关系,一次函数关系 |
如图,在矩形 中, ,点 在边 上,连接 ,以 为边向右上方作正方形 ,作 ,垂足为 ,连接 .
(1)求证: ;
(2)当 为何值时, 的面积最大?
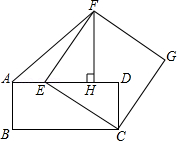
如图,以原点 为圆心,3为半径的圆与 轴分别交于 , 两点(点 在点 的右边), 是半径 上一点,过 且垂直于 的直线与 分别交于 , 两点(点 在点 的上方),直线 , 交于点 .若 .
(1)求点 的坐标;
(2)求过点 和点 ,且顶点在直线 上的抛物线的函数表达式.

2020年新冠肺炎疫情期间,部分药店趁机将口罩涨价,经调查发现某药店某月(按30天计)前5天的某型号口罩销售价格 (元 只)和销量 (只 与第 天的关系如下表:
| 第 天 |
1 |
2 |
3 |
4 |
5 |
| 销售价格 (元 只) |
2 |
3 |
4 |
5 |
6 |
| 销量 (只 |
70 |
75 |
80 |
85 |
90 |
物价部门发现这种乱象后,统一规定各药店该型号口罩的销售价格不得高于1元 只,该药店从第6天起将该型号口罩的价格调整为1元 只.据统计,该药店从第6天起销量 (只 与第 天的关系为 ,且 为整数),已知该型号口罩的进货价格为0.5元 只.
(1)直接写出该药店该月前5天的销售价格 与 和销量 与 之间的函数关系式;
(2)求该药店该月销售该型号口罩获得的利润 (元 与 的函数关系式,并判断第几天的利润最大;
(3)物价部门为了进一步加强市场整顿,对此药店在这个月销售该型号口罩的过程中获得的正常利润之外的非法所得部分处以 倍的罚款,若罚款金额不低于2000元,则 的取值范围为 .
如图所示,已知 中, , 边上的高 , 为 上一点, ,交 于点 ,交 于点 ,设点 到边 的距离为 .则 的面积 关于 的函数图象大致为

A. B.
B.
C. D.
D.
如图,矩形 中, 是 的中点,将 沿 翻折,点 落在点 处, .设 , 的面积为 ,则 与 的函数图象大致为

A. B.
B.
C.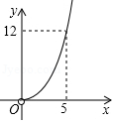 D.
D.
(年贵州省黔南州)为了解都匀市交通拥堵情况,经统计分析,都匀彩虹桥上的车流速度v(千米/时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/时;当车流密度为20辆/千米时,车流速度为80千米/时.研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数.
(1)求彩虹桥上车流密度为100辆/千米时的车流速度;
(2)在交通高峰时段,为使彩虹桥上车流速度大于40千米/时且小于60千米/时,应控制彩虹桥上的车流密度在什么范围内?
(3)当车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.当20≤x≤220时,求彩虹桥上车流量y的最大值.
某农作物的生长率与温度
有如下关系:如图,当
时可近似用函数
刻画;当
时可近似用函数
刻画.
(1)求的值.
(2)按照经验,该作物提前上市的天数(天
与生长率
之间满足已学过的函数关系,部分数据如下:
生长率 |
0.2 |
0.25 |
0.3 |
0.35 |
提前上市的天数 |
0 |
5 |
10 |
15 |
求:①关于
的函数表达式;
②用含的代数式表示
.
③天气寒冷,大棚加温可改变农作物生长速度.大棚恒温时每天的成本为100元,计划该作物30天后上市,现根据市场调查:每提前一天上市售出(一次售完),销售额可增加600元.因此决定给大棚继续加温,但加温导致成本增加,估测加温到
时的成本为200元
天,但若欲加温到
,由于要采用特殊方法,成本增加到400元
天.问加温到多少度时增加的利润最大?并说明理由.(注
农作物上市售出后大棚暂停使用)

某宾馆有若干间标准房,当标准房的价格为200元时,每天入住的房间数为60间.经市场调查表明,该馆每间标准房的价格在元之间(含170元,240元)浮动时,每天入住的房间数
(间
与每间标准房的价格
(元
的数据如下表:
|
190 |
200 |
210 |
220 |
||
|
65 |
60 |
55 |
50 |
(1)根据所给数据在坐标系中描出相应的点,并画出图象.
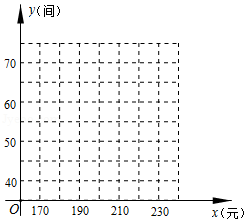
(2)求关于
的函数表达式,并写出自变量
的取值范围.
(3)设客房的日营业额为(元
.若不考虑其他因素,问宾馆标准房的价格定为多少元时,客房的日营业额最大?最大为多少元?
如图,点 、 、 、 是正方形 四条边(不含端点)上的点, 设线段 的长为 ,四边形 的面积为 ,则能够反映 与 之间函数关系的图象大致是

| A. |
|
B. |
|
| C. |
|
D. |
|
如图,在 中, , , ,点 是 边上的动点(不与点 重合),过 作 ,垂足为 ,点 是 的中点,连接 ,设 , 的面积为 ,则 与 之间的函数关系式为 .

北中环桥是省城太原的一座跨汾河大桥(如图 ,它由五个高度不同,跨径也不同的抛物线型钢拱通过吊桥,拉索与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象 抛物线)在同一竖直平面内,与拱脚所在的水平面相交于 , 两点.拱高为78米(即最高点 到 的距离为78米),跨径为90米(即 米),以最高点 为坐标原点,以平行于 的直线为 轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在直角坐标系 中,菱形 的边 在 轴正半轴上,点 , 在第一象限, ,边长 .点 从原点 出发沿 轴正半轴以每秒1个单位长的速度作匀速运动,点 从 出发沿边 以每秒2个单位长的速度作匀速运动,过点 作直线 垂直于 轴并交折线 于 ,交对角线 于 ,点 和点 同时出发,分别沿各自路线运动,点 运动到原点 时, 和 两点同时停止运动.
(1)当 时,求线段 的长;
(2)求 为何值时,点 与 重合;
(3)设 的面积为 ,求 与 的函数关系式及 的取值范围.

试题篮
()