初中数学二次函数的应用选择题

如图，线段 $\mathit{AB}=10$ ，点 $C$ 、 $D$ 在 $\mathit{AB}$ 上， $\mathit{AC}=\mathit{BD}=1$ ．已知点 $P$ 从点 $C$ 出发，以每秒1个单位长度的速度沿着 $\mathit{AB}$ 向点 $D$ 移动，到达点 $D$ 后停止移动．在点 $P$ 移动过程中作如下操作：先以点 $P$ 为圆心， $\mathit{PA}$ 、 $\mathit{PB}$ 的长为半径分别作两个圆心角均为 $60°$ 的扇形，再把两个扇形分别围成两个圆锥的侧面，设点 $P$ 的移动时间为 $t$ （秒 $)$ ，两个圆锥的底面面积之和为 $S$ ，则 $S$ 关于 $t$ 的函数图象大致是 $($ 　　 $)$

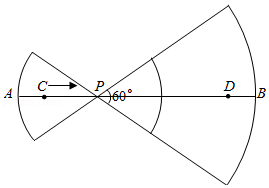
A．		B．
C．		D．

竖直上抛物体离地面的高度 $h\left(m\right)$与运动时间 $t\left(s\right)$之间的关系可以近似地用公式 $h=-5t^2+v_{0}t+h_0$表示，其中 $h_0\left(m\right)$是物体抛出时离地面的高度， $v_0(m/s)$是物体抛出时的速度．某人将一个小球从距地面 $1.5m$的高处以 $20m/s$的速度竖直向上抛出，小球达到的离地面的最大高度为 $($　　 $)$

A． $23.5m$B． $22.5m$C． $21.5m$D． $20.5m$

已知学校航模组设计制作的火箭的升空高度 $h\left(m\right)$与飞行时间 $t\left(s\right)$满足函数表达式 $h=-t^2+24t+1$．则下列说法中正确的是 $($　　 $)$

A．点火后 $9s$和点火后 $13s$的升空高度相同

B．点火后 $24s$火箭落于地面

C．点火后 $10s$的升空高度为 $139m$

D．火箭升空的最大高度为 $145m$

在平面直角坐标系 $\mathit{xOy}$中，已知点 $M$， $N$的坐标分别为 $(-1,2)$， $(2,1)$，若抛物线 $y=a{x}^2-x+2(a\ne 0)$与线段 $\mathit{MN}$有两个不同的交点，则 $a$的取值范围是 $($　　 $)$

A． $a⩽-1$或 $\frac{1}{4}⩽a<\frac{1}{3}$B． $\frac{1}{4}⩽a<\frac{1}{3}$

C． $a⩽\frac{1}{4}$或 $a>\frac{1}{3}$D． $a⩽-1$或 $a⩾\frac{1}{4}$

如图，在 $\mathit{\Delta ABC}$中， $\angle \mathit{ACB}=90°$， $\mathit{AC}=4$， $\mathit{BC}=2$． $P$是 $\mathit{AB}$边上一动点， $\mathit{PD}\perp \mathit{AC}$于点 $D$，点 $E$在 $P$的右侧，且 $\mathit{PE}=1$，连接 $\mathit{CE}$． $P$从点 $A$出发，沿 $\mathit{AB}$方向运动，当 $E$到达点 $B$时， $P$停止运动．在整个运动过程中，图中阴影部分面积 $S_1+S_2$的大小变化情况是 $($　　 $)$

A．一直减小B．一直不变C．先减小后增大D．先增大后减小

一位篮球运动员在距离篮圈中心水平距离 $4m$处起跳投篮，球沿一条抛物线运动，当球运动的水平距离为 $2.5m$时，达到最大高度 $3.5m$，然后准确落入篮筐内．已知篮圈中心距离地面高度为 $3.05m$，在如图所示的平面直角坐标系中，下列说法正确的是 $($　　 $)$

A．此抛物线的解析式是 $y=-\frac{1}{5}{x}^2+3.5$

B．篮圈中心的坐标是 $(4,3.05)$

C．此抛物线的顶点坐标是 $(3.5,0)$

D．篮球出手时离地面的高度是 $2m$

如图，矩形 $\mathit{ABCD}$中， $\mathit{AB}=8\mathit{cm}$， $\mathit{BC}=6\mathit{cm}$，点 $P$从点 $A$出发，以 $1\mathit{cm}/s$的速度沿 $A\to D\to C$方向匀速运动，同时点 $Q$从点 $A$出发，以 $2\mathit{cm}/s$的速度沿 $A\to B\to C$方向匀速运动，当一个点到达点 $C$时，另一个点也随之停止．设运动时间为 $t\left(s\right)$， $\mathit{\Delta APQ}$的面积为 $S\left(c{m}^2\right)$，下列能大致反映 $S$与 $t$之间函数关系的图象是 $($　　 $)$

A．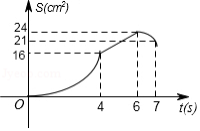

B．

C．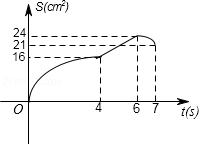

D．

如图，将一个小球从斜坡的点 $O$处抛出，小球的抛出路线可以用二次函数 $y=4x-\frac{1}{2}{x}^2$刻画，斜坡可以用一次函数 $y=\frac{1}{2}x$刻画，下列结论错误的是 $($　　 $)$

A．当小球抛出高度达到 $7.5m$时，小球距 $O$点水平距离为 $3m$

B．小球距 $O$点水平距离超过4米呈下降趋势

C．小球落地点距 $O$点水平距离为7米

D．斜坡的坡度为 $1:2$

如图，在 $\mathit{\Delta ABC}$中， $\angle B=90°$， $\mathit{AB}=3\mathit{cm}$， $\mathit{BC}=6\mathit{cm}$，动点 $P$从点 $A$开始沿 $\mathit{AB}$向点 $B$以 $1\mathit{cm}/s$的速度移动，动点 $Q$从点 $B$开始沿 $\mathit{BC}$向点 $C$以 $2\mathit{cm}/s$的速度移动，若 $P$， $Q$两点分别从 $A$， $B$两点同时出发， $P$点到达 $B$点运动停止，则 $\mathit{\Delta PBQ}$的面积 $S$随出发时间 $t$的函数图象大致是 $($　　 $)$

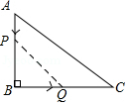
A．B．

C．D．

三孔桥横截面的三个孔都呈抛物线形，两小孔形状、大小完全相同．当水面刚好淹没小孔时，大孔水面宽度为10米，孔顶离水面1.5米；当水位下降，大孔水面宽度为14米时，单个小孔的水面宽度为4米，若大孔水面宽度为20米，则单个小孔的水面宽度为 $($　　 $)$

A． $4\sqrt{3}$米B． $5\sqrt{2}$米C． $2\sqrt{13}$米D．7米

某宾馆共有80间客房．宾馆负责人根据经验作出预测：今年7月份，每天的房间空闲数 $y$（间）与定价 $x$（元 $/$间）之间满足 $y=\frac{1}{4}x-42(x⩾168)$．若宾馆每天的日常运营成本为5000元，有客人入住的房间，宾馆每天每间另外还需支出28元的各种费用，宾馆想要获得最大利润，同时也想让客人得到实惠，应将房间定价确定为 $($　　 $)$

A．252元 $/$间B．256元 $/$间C．258元 $/$间D．260元 $/$间

如图是王阿姨晚饭后步行的路程 $S$（单位： $m)$与时间 $t$（单位： $\mathit{min})$的函数图象，其中曲线段 $\mathit{AB}$是以 $B$为顶点的抛物线一部分．下列说法不正确的是 $($　　 $)$

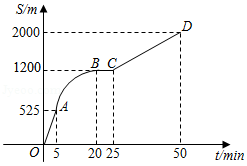
A． $25\mathit{min}~50\mathit{min}$，王阿姨步行的路程为 $800m$

B．线段 $\mathit{CD}$的函数解析式为 $S=32t+400(25⩽t⩽50)$

C． $5\mathit{min}~20\mathit{min}$，王阿姨步行速度由慢到快

D．曲线段 $\mathit{AB}$的函数解析式为 $S=-3{(t-20)}^2+1200(5⩽t⩽20)$

如图，利用一个直角墙角修建一个梯形储料场 $\mathit{ABCD}$，其中 $\angle C=120°$．若新建墙 $\mathit{BC}$与 $\mathit{CD}$总长为 $12m$，则该梯形储料场 $\mathit{ABCD}$的最大面积是 $($　　 $)$

A． $18m^2$B． $18\sqrt{3}{m}^2$C． $24\sqrt{3}{m}^2$D． $\frac{45\sqrt{3}}{2}{m}^2$

如图，在 $\mathit{\Delta ABC}$中， $\angle B=90°$， $\tan \angle C=\frac{3}{4}$， $\mathit{AB}=6\mathit{cm}$．动点 $P$从点 $A$开始沿边 $\mathit{AB}$向点 $B$以 $1\mathit{cm}/s$的速度移动，动点 $Q$从点 $B$开始沿边 $\mathit{BC}$向点 $C$以 $2\mathit{cm}/s$的速度移动．若 $P$， $Q$两点分别从 $A$， $B$两点同时出发，在运动过程中， $\mathit{\Delta PBQ}$的最大面积是 $($　　 $)$

A． $18c{m}^2$B． $12c{m}^2$C． $9c{m}^2$D． $3c{m}^2$

一列自然数0，1，2，3， $\dots$，100．依次将该列数中的每一个数平方后除以100，得到一列新数．则下列结论正确的是 $($　　 $)$

A．原数与对应新数的差不可能等于零

B．原数与对应新数的差，随着原数的增大而增大

C．当原数与对应新数的差等于21时，原数等于30

D．当原数取50时，原数与对应新数的差最大