初中数学二次函数的应用解答题

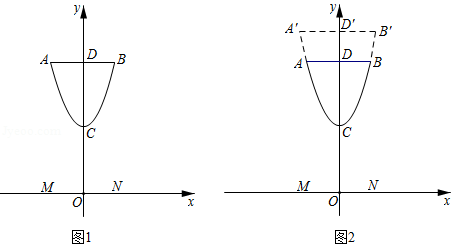
小聪设计奖杯，从抛物线形状上获得灵感，在平面直角坐标系中画出截面示意图，如图1，杯体 $\mathit{ACB}$ 是抛物线的一部分，抛物线的顶点 $C$ 在 $y$ 轴上，杯口直径 $\mathit{AB}=4$ ，且点 $A$ ， $B$ 关于 $y$ 轴对称，杯脚高 $\mathit{CO}=4$ ，杯高 $\mathit{DO}=8$ ，杯底 $\mathit{MN}$ 在 $x$ 轴上．

（1）求杯体 $\mathit{ACB}$ 所在抛物线的函数表达式（不必写出 $x$ 的取值范围）；

（2）为使奖杯更加美观，小敏提出了改进方案，如图2，杯体 $A\text{'}\mathit{CB}\text{'}$ 所在抛物线形状不变，杯口直径 $A\text{'}B\text{'}//\mathit{AB}$ ，杯脚高 $\mathit{CO}$ 不变，杯深 $\mathit{CD}\text{'}$ 与杯高 $\mathit{OD}\text{'}$ 之比为0.6，求 $A\text{'}B\text{'}$ 的长．

某游乐场的圆形喷水池中心 $O$ 有一雕塑 $\mathit{OA}$ ，从 $A$ 点向四周喷水，喷出的水柱为抛物线，且形状相同．如图，以水平方向为 $x$ 轴，点 $O$ 为原点建立直角坐标系，点 $A$ 在 $y$ 轴上， $x$ 轴上的点 $C$ ， $D$ 为水柱的落水点，水柱所在抛物线（第一象限部分）的函数表达式为 $y=-\frac{1}{6}{(x-5)}^2+6$ ．

（1）求雕塑高 $\mathit{OA}$ ．

（2）求落水点 $C$ ， $D$ 之间的距离．

（3）若需要在 $\mathit{OD}$ 上的点 $E$ 处竖立雕塑 $\mathit{EF}$ ， $\mathit{OE}=10m$ ， $\mathit{EF}=1.8m$ ， $\mathit{EF}\perp \mathit{OD}$ ．问：顶部 $F$ 是否会碰到水柱？请通过计算说明．

今年以来，我市接待的游客人数逐月增加，据统计，游玩某景区的游客人数三月份为4万人，五月份为5.76万人．

（1）求四月和五月这两个月中该景区游客人数平均每月增长百分之几；

（2）若该景区仅有 $A$ ， $B$ 两个景点，售票处出示的三种购票方式如下表所示：

购票方式	甲	乙	丙
可游玩景点	$A$	$B$	$A$ 和     $B$
门票价格	100元     $/$ 人	80元     $/$ 人	160元     $/$ 人

据预测，六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万，并且当甲、乙两种门票价格不变时，丙种门票价格每下降1元，将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票．

①若丙种门票价格下降10元，求景区六月份的门票总收入；

②问：将丙种门票价格下降多少元时，景区六月份的门票总收入有最大值？最大值是多少万元？

某药店选购了一批消毒液，进价为每瓶10元，在销售过程中发现，每天销售量 $y$（瓶 $)$与每瓶售价 $x$（元 $)$之间存在一次函数关系（其中 $10⩽x⩽21$，且 $x$为整数）．当每瓶消毒液售价为12元时，每天销售量为90瓶；当每瓶消毒液售价为15元时，每天销售量为75瓶．

（1）求 $y$与 $x$之间的函数关系式；

（2）设该药店销售该消毒液每天的销售利润为 $w$元，当每瓶消毒液售价为多少元时，药店销售该消毒液每天销售利润最大，最大利润是多少元？

某服装店以每件30元的价格购进一批 $T$恤，如果以每件40元出售，那么一个月内能售出300件，根据以往销售经验，销售单价每提高1元，销售量就会减少10件，设 $T$恤的销售单价提高 $x$元．

（1）服装店希望一个月内销售该种 $T$恤能获得利润3360元，并且尽可能减少库存，问 $T$恤的销售单价应提高多少元？

（2）当销售单价定为多少元时，该服装店一个月内销售这种 $T$恤获得的利润最大？最大利润是多少元？

渠县是全国优质黄花主产地，某加工厂加工黄花的成本为30元 $/$千克，根据市场调查发现，批发价定为48元 $/$千克时，每天可销售500千克，为增大市场占有率，在保证盈利的情况下，工厂采取降价措施，批发价每千克降低1元，每天销量可增加50千克．

（1）写出工厂每天的利润 $W$元与降价 $x$元之间的函数关系．当降价2元时，工厂每天的利润为多少元？

（2）当降价多少元时，工厂每天的利润最大，最大为多少元？

（3）若工厂每天的利润要达到9750元，并让利于民，则定价应为多少元？

某商场购进甲、乙两种商品共100箱，全部售完后，甲商品共盈利900元，乙商品共盈利400元，甲商品比乙商品每箱多盈利5元．

（1）求甲、乙两种商品每箱各盈利多少元？

（2）甲、乙两种商品全部售完后，该商场又购进一批甲商品，在原每箱盈利不变的前提下，平均每天可卖出100箱．如调整价格，每降价1元，平均每天可多卖出20箱，那么当降价多少元时，该商场利润最大？最大利润是多少？

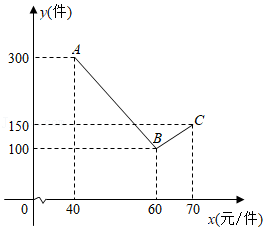
某商家正在热销一种商品，其成本为30元 $/$ 件，在销售过程中发现随着售价增加，销售量在减少．商家决定当售价为60元 $/$ 件时，改变销售策略，此时售价每增加1元需支付由此产生的额外费用150元．该商品销售量 $y$ （件 $)$ 与售价 $x$ （元 $/$ 件）满足如图所示的函数关系（其中 $40⩽x⩽70$ ，且 $x$ 为整数）．

（1）写出 $y$ 与 $x$ 的函数关系式；

（2）当售价为多少时，商家所获利润最大，最大利润是多少？

因疫情防控需要，消毒用品需求量增加．某药店新进一批桶装消毒液，每桶进价50元，每天销售量 $y$（桶 $)$与销售单价 $x$（元 $)$之间满足一次函数关系，其图象如图所示．

（1）求 $y$与 $x$之间的函数表达式；

（2）每桶消毒液的销售价定为多少元时，药店每天获得的利润最大，最大利润是多少元？（利润 $=$销售价 $-$进价）

某水果商店销售一种进价为40元 $/$千克的优质水果，若售价为50元 $/$千克，则一个月可售出500千克；若售价在50元 $/$千克的基础上每涨价1元，则月销售量就减少10千克．

（1）当售价为55元 $/$千克时，每月销售水果多少千克？

（2）当月利润为8750元时，每千克水果售价为多少元？

（3）当每千克水果售价为多少元时，获得的月利润最大？

如图1，排球场长为 $18m$，宽为 $9m$，网高为 $2.24m$，队员站在底线 $O$点处发球，球从点 $O$的正上方 $1.9m$的 $C$点发出，运动路线是抛物线的一部分，当球运动到最高点 $A$时，高度为 $2.88m$，即 $\mathit{BA}=2.88m$，这时水平距离 $\mathit{OB}=7m$，以直线 $\mathit{OB}$为 $x$轴，直线 $\mathit{OC}$为 $y$轴，建立平面直角坐标系，如图2．

（1）若球向正前方运动（即 $x$轴垂直于底线），求球运动的高度 $y\left(m\right)$与水平距离 $x\left(m\right)$之间的函数关系式（不必写出 $x$取值范围）．并判断这次发球能否过网？是否出界？说明理由．

（2）若球过网后的落点是对方场地①号位内的点 $P$（如图1，点 $P$距底线 $1m$，边线 $0.5m)$，问发球点 $O$在底线上的哪个位置？（参考数据： $\sqrt{2}$取 $1.4)$

如图1，在平面直角坐标系中， $\mathit{\Delta ABC}$的顶点 $A$， $C$分别是直线 $y=-\frac{8}{3}x+4$与坐标轴的交点，点 $B$的坐标为 $(-2,0)$，点 $D$是边 $\mathit{AC}$上的一点， $\mathit{DE}\perp \mathit{BC}$于点 $E$，点 $F$在边 $\mathit{AB}$上，且 $D$， $F$两点关于 $y$轴上的某点成中心对称，连结 $\mathit{DF}$， $\mathit{EF}$．设点 $D$的横坐标为 $m$， $E{F}^2$为 $l$，请探究：

①线段 $\mathit{EF}$长度是否有最小值．

② $\mathit{\Delta BEF}$能否成为直角三角形．

小明尝试用“观察 $-$猜想 $-$验证 $-$应用”的方法进行探究，请你一起来解决问题．

（1）小明利用“几何画板”软件进行观察，测量，得到 $l$随 $m$变化的一组对应值，并在平面直角坐标系中以各对应值为坐标描点（如图 $2)$．请你在图2中连线，观察图象特征并猜想 $l$与 $m$可能满足的函数类别．

（2）小明结合图1，发现应用三角形和函数知识能验证（1）中的猜想，请你求出 $l$关于 $m$的函数表达式及自变量的取值范围，并求出线段 $\mathit{EF}$长度的最小值．

（3）小明通过观察，推理，发现 $\mathit{\Delta BEF}$能成为直角三角形，请你求出当 $\mathit{\Delta BEF}$为直角三角形时 $m$的值．

“扬州漆器”名扬天下，某网店专门销售某种品牌的漆器笔筒，成本为30元 $/$件，每天销售 $y$（件 $)$与销售单价 $x$（元 $)$之间存在一次函数关系，如图所示．

（1）求 $y$与 $x$之间的函数关系式；

（2）如果规定每天漆器笔筒的销售量不低于240件，当销售单价为多少元时，每天获取的利润最大，最大利润是多少？

（3）该网店店主热心公益事业，决定从每天的销售利润中捐出150元给希望工程，为了保证捐款后每天剩余利润不低于3600元，试确定该漆器笔筒销售单价的范围．

某景区商店销售一种纪念品，每件的进货价为40元．经市场调研，当该纪念品每件的销售价为50元时，每天可销售200件；当每件的销售价每增加1元，每天的销售数量将减少10件．

（1）当每件的销售价为52元时，该纪念品每天的销售数量为　　件；

（2）当每件的销售价 $x$为多少时，销售该纪念品每天获得的利润 $y$最大？并求出最大利润．

某乡镇实施产业扶贫，帮助贫困户承包了荒山种植某品种蜜柚，到了收获季节，已知该蜜柚的成本价为8元 $/$千克，投入市场销售时，调查市场行情，发现该蜜柚销售不会亏本，且每天销售量 $y$（千克）与销售单价 $x$（元 $/$千克）之间的函数关系如图所示．

（1）求 $y$与 $x$的函数关系式，并写出 $x$的取值范围；

（2）当该品种的蜜柚定价为多少时，每天销售获得的利润最大？最大利润是多少？

（3）某农户今年共采摘蜜柚4800千克，该品种蜜柚的保质期为40天，根据（2）中获得最大利润的方式进行销售，能否销售完这批蜜柚？请说明理由．