初中数学二次函数的应用解答题

温州某企业安排65名工人生产甲、乙两种产品，每人每天生产2件甲或1件乙，甲产品每件可获利15元．根据市场需求和生产经验，乙产品每天产量不少于5件，当每天生产5件时，每件可获利120元，每增加1件，当天平均每件利润减少2元．设每天安排 $x$人生产乙产品．

（1）根据信息填表：

产品种类	每天工人数（人 $)$	每天产量（件 $)$	每件产品可获利润（元 $)$
甲			15
乙	$x$	$x$

（2）若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元，求每件乙产品可获得的利润．

（3）该企业在不增加工人的情况下，增加生产丙产品，要求每天甲、丙两种产品的产量相等．已知每人每天可生产1件丙（每人每天只能生产一件产品），丙产品每件可获利30元，求每天生产三种产品可获得的总利润 $W$（元 $)$的最大值及相应的 $x$值．

某药厂销售部门根据市场调研结果，对该厂生产的一种新型原料药未来两年的销售进行预测，并建立如下模型：设第 $t$个月该原料药的月销售量为 $P$（单位：吨）， $P$与 $t$之间存在如图所示的函数关系，其图象是函数 $P=\frac{120}{t+4}(0<t⩽8)$的图象与线段 $\mathit{AB}$的组合；设第 $t$个月销售该原料药每吨的毛利润为 $Q$（单位：万元）， $Q$与 $t$之间满足如下关系： $Q=\left\{\begin{array}{c}2t+8,0<t⩽12\\ -t+44,12<t⩽24\end{array}\right.$

（1）当 $8<t⩽24$时，求 $P$关于 $t$的函数解析式；

（2）设第 $t$个月销售该原料药的月毛利润为 $w$（单位：万元）

①求 $w$关于 $t$的函数解析式；

②该药厂销售部门分析认为， $336⩽w⩽513$是最有利于该原料药可持续生产和销售的月毛利润范围，求此范围所对应的月销售量 $P$的最小值和最大值．

学校拓展小组研制了绘图智能机器人（如图 $1)$，顺次输入点 $P_1$， $P_2$， $P_3$的坐标，机器人能根据图2，绘制图形．若图形是线段，求出线段的长度；若图形是抛物线，求出抛物线的函数关系式．请根据以下点的坐标，求出线段的长度或抛物线的函数关系式．

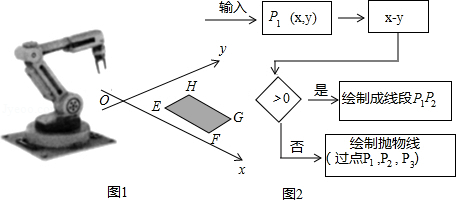
（1） $P_1(4,0)$， $P_2(0,0)$， $P_3(6,6)$；

（2） $P_1(0,0)$， $P_2(4,0)$， $P_3(6,6)$．

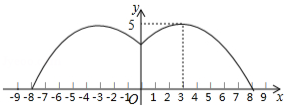
某游乐园有一个直径为16米的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为抛物线，在距水池中心3米处达到最高，高度为5米，且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合．如图所示，以水平方向为 $x$轴，喷水池中心为原点建立直角坐标系．

（1）求水柱所在抛物线（第一象限部分）的函数表达式；

（2）王师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心多少米以内？

（3）经检修评估，游乐园决定对喷水设施做如下设计改进：在喷出水柱的形状不变的前提下，把水池的直径扩大到32米，各方向喷出的水柱仍在喷水池中心保留的原装饰物（高度不变）处汇合，请探究扩建改造后喷水池水柱的最大高度．

交通工程学理论把在单向道路上行驶的汽车看成连续的流体，并用流量、速度、密度三个概念描述车流的基本特征．其中流量 $q$（辆 $/$小时）指单位时间内通过道路指定断面的车辆数；速度 $v$（千米 $/$小时）指通过道路指定断面的车辆速度；密度 $k$（辆 $/$千米）指通过道路指定断面单位长度内的车辆数．

为配合大数据治堵行动，测得某路段流量 $q$与速度 $v$之间关系的部分数据如下表：

速度 $v$（千米 $/$小时）	$\dots$	5	10	20	32	40	48	$\dots$
流量 $q$（辆 $/$小时）	$\dots$	550	1000	1600	1792	1600	1152	$\dots$

（1）根据上表信息，下列三个函数关系式中，刻画 $q$， $v$关系最准确的是　　（只填上正确答案的序号）

① $q=90v+100$；② $q=\frac{32000}{v}$；③ $q=-2v^2+120v$．

（2）请利用（1）中选取的函数关系式分析，当该路段的车流速度为多少时，流量达到最大？最大流量是多少？

（3）已知 $q$， $v$， $k$满足 $q=\mathit{vk}$，请结合（1）中选取的函数关系式继续解决下列问题．

①市交通运行监控平台显示，当 $12⩽v<18$时道路出现轻度拥堵．试分析当车流密度 $k$在什么范围时，该路段将出现轻度拥堵；

②在理想状态下，假设前后两车车头之间的距离 $d$（米 $)$均相等，求流量 $q$最大时 $d$的值．

如图1，在 $\mathit{\Delta ABC}$中， $\angle A=30°$，点 $P$从点 $A$出发以 $2\mathit{cm}/s$的速度沿折线 $A-C-B$运动，点 $Q$从点 $A$出发以 $a(\mathit{cm}/s)$的速度沿 $\mathit{AB}$运动， $P$， $Q$两点同时出发，当某一点运动到点 $B$时，两点同时停止运动．设运动时间为 $x\left(s\right)$， $\mathit{\Delta APQ}$的面积为 $y\left(c{m}^2\right)$， $y$关于 $x$的函数图象由 $C_1$， $C_2$两段组成，如图2所示．

（1）求 $a$的值；

（2）求图2中图象 $C_2$段的函数表达式；

（3）当点 $P$运动到线段 $\mathit{BC}$上某一段时 $\mathit{\Delta APQ}$的面积，大于当点 $P$在线段 $\mathit{AC}$上任意一点时 $\mathit{\Delta APQ}$的面积，求 $x$的取值范围．

甲、乙两人进行羽毛球比赛，羽毛球飞行的路线为抛物线的一部分，如图，甲在 $O$点正上方 $1m$的 $P$处发出一球，羽毛球飞行的高度 $y\left(m\right)$与水平距离 $x\left(m\right)$之间满足函数表达式 $y=a{(x-4)}^2+h$，已知点 $O$与球网的水平距离为 $5m$，球网的高度为 $1.55m$．

（1）当 $a=-\frac{1}{24}$时，①求 $h$的值；②通过计算判断此球能否过网．

（2）若甲发球过网后，羽毛球飞行到与点 $O$的水平距离为 $7m$，离地面的高度为 $\frac{12}{5}m$的 $Q$处时，乙扣球成功，求 $a$的值．

某农场拟建一间矩形种牛饲养室，饲养室的一面靠现有墙（墙足够长），已知计划中的建筑材料可建围墙的总长为 $50m$．设饲养室长为 $x\left(m\right)$，占地面积为 $y\left(m^2\right)$．

（1）如图1，问饲养室长 $x$为多少时，占地面积 $y$最大？

（2）如图2，现要求在图中所示位置留 $2m$宽的门，且仍使饲养室的占地面积最大，小敏说：“只要饲养室长比（1）中的长多 $2m$就行了．”请你通过计算，判断小敏的说法是否正确．

湖州素有鱼米之乡之称，某水产养殖大户为了更好地发挥技术优势，一次性收购了 $20000\mathit{kg}$淡水鱼，计划养殖一段时间后再出售．已知每天放养的费用相同，放养10天的总成本为30.4万元；放养20天的总成本为30.8万元（总成本 $=$放养总费用 $+$收购成本）．

（1）设每天的放养费用是 $a$万元，收购成本为 $b$万元，求 $a$和 $b$的值；

（2）设这批淡水鱼放养 $t$天后的质量为 $m\left(\mathit{kg}\right)$，销售单价为 $y$元 $/\mathit{kg}$．根据以往经验可知： $m$与 $t$的函数关系为 $m=\left\{\begin{array}{c}20000(0⩽t⩽50)\\ 100t+15000(50<t⩽100)\end{array}\right.$； $y$与 $t$的函数关系如图所示．

①分别求出当 $0⩽t⩽50$和 $50<t⩽100$时， $y$与 $t$的函数关系式；

②设将这批淡水鱼放养 $t$天后一次性出售所得利润为 $W$元，求当 $t$为何值时， $W$最大？并求出最大值．（利润 $=$销售总额 $-$总成本）

如图1，地面 $\mathit{BD}$上两根等长立柱 $\mathit{AB}$， $\mathit{CD}$之间悬挂一根近似成抛物线 $y=\frac{1}{10}{x}^2-\frac{4}{5}x+3$的绳子．

（1）求绳子最低点离地面的距离；

（2）因实际需要，在离 $\mathit{AB}$为3米的位置处用一根立柱 $\mathit{MN}$撑起绳子（如图 $2)$，使左边抛物线 $F_1$的最低点距 $\mathit{MN}$为1米，离地面1.8米，求 $\mathit{MN}$的长；

（3）将立柱 $\mathit{MN}$的长度提升为3米，通过调整 $\mathit{MN}$的位置，使抛物线 $F_2$对应函数的二次项系数始终为 $\frac{1}{4}$，设 $\mathit{MN}$离 $\mathit{AB}$的距离为 $m$，抛物线 $F_2$的顶点离地面距离为 $k$，当 $2⩽k⩽2.5$时，求 $m$的取值范围．

如图1，地面 $\mathit{BD}$上两根等长立柱 $\mathit{AB}$， $\mathit{CD}$之间悬挂一根近似成抛物线 $y=\frac{1}{10}{x}^2-\frac{4}{5}x+3$的绳子．

（1）求绳子最低点离地面的距离；

（2）因实际需要，在离 $\mathit{AB}$为3米的位置处用一根立柱 $\mathit{MN}$撑起绳子（如图 $2)$，使左边抛物线 $F_1$的最低点距 $\mathit{MN}$为1米，离地面1.8米，求 $\mathit{MN}$的长；

（3）将立柱 $\mathit{MN}$的长度提升为3米，通过调整 $\mathit{MN}$的位置，使抛物线 $F_2$对应函数的二次项系数始终为 $\frac{1}{4}$，设 $\mathit{MN}$离 $\mathit{AB}$的距离为 $m$，抛物线 $F_2$的顶点离地面距离为 $k$，当 $2⩽k⩽2.5$时，求 $m$的取值范围．

课本中有一个例题：

有一个窗户形状如图1，上部是一个半圆，下部是一个矩形，如果制作窗框的材料总长为 $6m$，如何设计这个窗户，使透光面积最大？

这个例题的答案是：当窗户半圆的半径约为 $0.35m$时，透光面积最大值约为 $1.05m^2$．

我们如果改变这个窗户的形状，上部改为由两个正方形组成的矩形，如图2，材料总长仍为 $6m$，利用图3，解答下列问题：

（1）若 $\mathit{AB}$为 $1m$，求此时窗户的透光面积？

（2）与课本中的例题比较，改变窗户形状后，窗户透光面积的最大值有没有变大？请通过计算说明．

把一个足球垂直水平地面向上踢，时间为 $t$（秒 $)$时该足球距离地面的高度 $h$（米 $)$适用公式 $h=20t-5t^2(0⩽t⩽4)$．

（1）当 $t=3$时，求足球距离地面的高度；

（2）当足球距离地面的高度为10米时，求 $t$；

（3）若存在实数 $t_1$， $t_2(t_1\ne t_2)$当 $t=t_1$或 $t_2$时，足球距离地面的高度都为 $m$（米 $)$，求 $m$的取值范围．

对于三个数 $a$， $b$， $c$，用 $M\{a$， $b$， $c\}$表示这三个数的中位数，用 $\mathit{max}\{a$， $b$， $c\}$表示这三个数中最大数，例如： $M\{-2$， $-1$， $0\}=-1$， $\mathit{max}\{-2$， $-1$， $0\}=0$， $\mathit{max}\{-2$， $-1$， $a\}=\left\{\begin{array}{c}a(a⩾-1)\\ -1(a<-1)\end{array}\right.$

解决问题：

（1）填空： $M\{\sin 45°$， $\cos 60°$， $\tan 60°\}=$　　，如果 $\mathit{max}\{3$， $5-3x$， $2x-6\}=3$，则 $x$的取值范围为　　；

（2）如果 $2·M\{2$， $x+2$， $x+4\}=\mathit{max}\{2$， $x+2$， $x+4\}$，求 $x$的值；

（3）如果 $M\{9$， $x^2$， $3x-2\}=\mathit{max}\{9$， $x^2$， $3x-2\}$，求 $x$的值．

传统的端午节即将来临，某企业接到一批粽子生产任务，约定这批粽子的出厂价为每只4元，按要求在20天内完成．为了按时完成任务，该企业招收了新工人，设新工人李明第 $x$天生产的粽子数量为 $y$只， $y$与 $x$满足如下关系：

$y=\left\{\begin{array}{c}34x(0⩽x⩽6)\\ 20x+80(6<x⩽20)\end{array}\right.$

（1）李明第几天生产的粽子数量为280只？

（2）如图，设第 $x$天生产的每只粽子的成本是 $p$元， $p$与 $x$之间的关系可用图中的函数图象来刻画．若李明第 $x$天创造的利润为 $w$元，求 $w$与 $x$之间的函数表达式，并求出第几天的利润最大？最大利润是多少元？（利润 $=$出厂价 $-$成本）