初中数学二次函数的应用解答题

某大学生创业团队抓住商机，购进一批干果分装成营养搭配合理的小包装后出售，每袋成本3元．试销期间发现每天的销售量 $y$（袋 $)$与销售单价 $x$（元 $)$之间满足一次函数关系，部分数据如表所示，其中 $3.5⩽x⩽5.5$，另外每天还需支付其他各项费用80元．

销售单价 $x$（元 $)$	3.5	5.5
销售量 $y$（袋 $)$	280	120

（1）请直接写出 $y$与 $x$之间的函数关系式；

（2）如果每天获得160元的利润，销售单价为多少元？

（3）设每天的利润为 $w$元，当销售单价定为多少元时，每天的利润最大？最大利润是多少元？

俄罗斯世界杯足球赛期间，某商店销售一批足球纪念册，每本进价40元，规定销售单价不低于44元，且获利不高于 $30\%$．试销售期间发现，当销售单价定为44元时，每天可售出300本，销售单价每上涨1元，每天销售量减少10本，现商店决定提价销售．设每天销售量为 $y$本，销售单价为 $x$元．

（1）请直接写出 $y$与 $x$之间的函数关系式和自变量 $x$的取值范围；

（2）当每本足球纪念册销售单价是多少元时，商店每天获利2400元？

（3）将足球纪念册销售单价定为多少元时，商店每天销售纪念册获得的利润 $w$元最大？最大利润是多少元？

某商场销售一种小商品，每件进货价为190元，调查发现，当销售价为210元时，平均每天能销售8件；当销售价每降低2元时，平均每天就能多销售4件，设每件小商品降价 $x$元，平均每天销售 $y$件．

（1）求 $y$与 $x$之间的函数关系式；

（2）商场要想使这种小商品平均每天的销售利润达到280元，求每件小商品的销售价应定为多少元？

（3）设每天的销售总利润为 $w$元，求 $w$与 $x$之间的函数关系式；每件小商品降价多少元时，每天的总利润最大？最大利润是多少？

【观察】 $1\times 49=49$， $2\times 48=96$， $3\times 47=141$， $\dots$， $23\times 27=621$， $24\times 26=624$， $25\times 25=625$， $26\times 24=624$， $27\times 23=621$， $\dots$， $47\times 3=141$， $48\times 2=96$， $49\times 1=49$．

【发现】根据你的阅读回答问题：

（1）上述内容中，两数相乘，积的最大值为　　；

（2）设参与上述运算的第一个因数为 $a$，第二个因数为 $b$，用等式表示 $a$与 $b$的数量关系是　　．

【类比】观察下列两数的积： $1\times 59$， $2\times 58$， $3\times 57$， $4\times 56$， $\dots$， $m\times n$， $\dots$， $56\times 4$， $57\times 3$， $58\times 2$， $59\times 1$．

猜想 $\mathit{mn}$的最大值为　　，并用你学过的知识加以证明．

某公司设计了一款产品，每件成本是50元，在试销期间，据市场调查，销售单价是60元时，每天的销量是250件，而销售单价每增加1元，每天会少售出5件，公司决定销售单价 $x$（元 $)$不低于60元，而市场要求 $x$不得超过100元．

（1）求出每天的销售量 $y$（件 $)$与销售单价 $x$（元 $)$之间的函数关系式，并写出 $x$的取值范围；

（2）求出每天的销售利润 $W$（元 $)$与销售单价 $x$（元 $)$之间的函数关系式，并求出当 $x$为多少时，每天的销售利润最大，并求出最大值；

（3）若该公司要求每天的销售利润不低于4000元，但每天的总成本不超过6250元，则销售单价 $x$最低可定为多少元？

服装厂批发某种服装，每件成本为65元，规定不低于10件可以批发，其批发价 $y$（元 $/$件）与批发数量 $x$（件 $\left)\right(x$为正整数）之间所满足的函数关系如图所示．

（1）求 $y$与 $x$之间所满足的函数关系式，并写出 $x$的取值范围；

（2）设服装厂所获利润为 $w$（元 $)$，若 $10⩽x⩽50(x$为正整数），求批发该种服装多少件时，服装厂获得利润最大？最大利润是多少元？

某公司去年年初投资1000万元引进先进的生产线生产某种新产品．根据对该产品的市场分析，生产每件该产品需成本60元，产品售价不超过200元 $/$件，且产品的年销售量 $y$（万件）是产品售价 $x$（元 $/$件）的一次函数，其部分对应数据如下表所示：

产品售价 $x$（元 $/$件）	$\dots$	120	140	160	180	$\dots$
销售量 $y$（万件）	$\dots$	9	8	7	6	$\dots$

（1）求 $y$关于 $x$的函数解析式；

（2）去年该公司是盈利还是亏损？并求出盈利最多或亏损最少时的产品售价；

（3）在（2）的前提下，若公司想使去年和今年生产的新产品共获利395万元，那么该公司今年应怎样重新确定产品售价？

如图，已知 $\mathit{AB}$为 $\odot O$的直径， $\mathit{AB}=8$，点 $C$和点 $D$是 $\odot O$上关于直线 $\mathit{AB}$对称的两个点，连接 $\mathit{OC}$、 $\mathit{AC}$，且 $\angle \mathit{BOC}<90°$，直线 $\mathit{BC}$和直线 $\mathit{AD}$相交于点 $E$，过点 $C$作直线 $\mathit{CG}$与线段 $\mathit{AB}$的延长线相交于点 $F$，与直线 $\mathit{AD}$相交于点 $G$，且 $\angle \mathit{GAF}=\angle \mathit{GCE}$．

（1）求证：直线 $\mathit{CG}$为 $\odot O$的切线；

（2）若点 $H$为线段 $\mathit{OB}$上一点，连接 $\mathit{CH}$，满足 $\mathit{CB}=\mathit{CH}$，

① $\mathit{\Delta CBH}\backsim \mathit{\Delta OBC}$；

②求 $\mathit{OH}+\mathit{HC}$的最大值．

如图1，在矩形 $\mathit{ABCD}$中， $E$是 $\mathit{AD}$的中点，以点 $E$为直角顶点的直角三角形 $\mathit{EFG}$的两边 $\mathit{EF}$， $\mathit{EG}$分别过点 $B$， $C$， $\angle F=30°$．

（1）求证： $\mathit{BE}=\mathit{CE}$；

（2）将 $\mathit{\Delta EFG}$绕点 $E$按顺时针方向旋转，当旋转到 $\mathit{EF}$与 $\mathit{AD}$重合时停止转动，若 $\mathit{EF}$， $\mathit{EG}$分别与 $\mathit{AB}$， $\mathit{BC}$相交于点 $M$， $N$（如图 $2)$．

①求证： $\mathit{\Delta BEM}\cong \mathit{\Delta CEN}$；

②若 $\mathit{AB}=2$，求 $\mathit{\Delta BMN}$面积的最大值；

③当旋转停止时，点 $B$恰好在 $\mathit{FG}$上（如图 $3)$，求 $\sin \angle \mathit{EBG}$的值．

一名在校大学生利用“互联网 $+$”自主创业，销售一种产品，这种产品的成本价10元 $/$件，已知销售价不低于成本价，且物价部门规定这种产品的销售价不高于16元 $/$件，市场调查发现，该产品每天的销售量 $y$（件 $)$与销售价 $x$（元 $/$件）之间的函数关系如图所示．

（1）求 $y$与 $x$之间的函数关系式，并写出自变量 $x$的取值范围；

（2）求每天的销售利润 $W$（元 $)$与销售价 $x$（元 $/$件）之间的函数关系式，并求出每件销售价为多少元时，每天的销售利润最大？最大利润是多少？

如图所示， $\text{Rt}\Delta \text{PAB}$的直角顶点 $P(3,4)$在函数 $y=\frac{k}{x}(x>0)$的图象上，顶点 $A$、 $B$在函数 $y=\frac{t}{x}(x>0,0<t<k)$的图象上， $\mathit{PA}//y$轴，连接 $\mathit{OP}$， $\mathit{OA}$，记 $\mathit{\Delta OPA}$的面积为 $S_{\mathit{\Delta OPA}}$， $\mathit{\Delta PAB}$的面积为 $S_{\mathit{\Delta PAB}}$，设 $w=S_{\mathit{\Delta OPA}}-S_{\mathit{\Delta PAB}}$．

①求 $k$的值以及 $w$关于 $t$的表达式；

②若用 $w_{\mathit{max}}$和 $w_{\mathit{min}}$分别表示函数 $w$的最大值和最小值，令 $T=w_{\mathit{max}}+a^2-a$，其中 $a$为实数，求 $T_{\mathit{min}}$．

若三个非零实数 $x$， $y$， $z$满足：只要其中一个数的倒数等于另外两个数的倒数的和，则称这三个实数 $x$， $y$， $z$构成“和谐三组数”．

（1）实数1，2，3可以构成“和谐三组数”吗？请说明理由；

（2）若 $M(t,y_1)$， $N(t+1,y_2)$， $R(t+3,y_3)$三点均在函数 $y=\frac{k}{x}(k$为常数， $k\ne 0)$的图象上，且这三点的纵坐标 $y_1$， $y_2$， $y_3$构成“和谐三组数”，求实数 $t$的值；

（3）若直线 $y=2\mathit{bx}+2c(\mathit{bc}\ne 0)$与 $x$轴交于点 $A(x_1$， $0)$，与抛物线 $y=a{x}^2+3\mathit{bx}+3c(a\ne 0)$交于 $B(x_2$， $y_2)$， $C(x_3$， $y_3)$两点．

①求证： $A$， $B$， $C$三点的横坐标 $x_1$， $x_2$， $x_3$构成“和谐三组数”；

②若 $a>2b>3c$， $x_2=1$，求点 $P(\frac{c}{a}$， $\frac{b}{a})$与原点 $O$的距离 $\mathit{OP}$的取值范围．

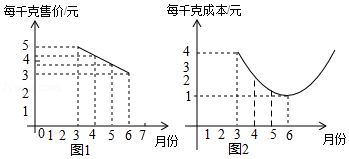
某种蔬菜的销售单价 $y_1$与销售月份 $x$之间的关系如图1所示，成本 $y_2$与销售月份 $x$之间的关系如图2所示（图1的图象是线段，图2的图象是抛物线）

（1）已知6月份这种蔬菜的成本最低，此时出售每千克的收益是多少元？（收益 $=$售价 $-$成本）

（2）哪个月出售这种蔬菜，每千克的收益最大？简单说明理由．

（3）已知市场部销售该种蔬菜4、5两个月的总收益为22万元，且5月份的销售量比4月份的销售量多2万千克，求4、5两个月的销售量分别是多少万千克？

六盘水市梅花山国际滑雪自建成以来，吸引大批滑雪爱好者，一滑雪者从山坡滑下，测得滑行距离 $y$（单位： $m)$与滑行时间 $x$（单位： $s)$之间的关系可以近似的用二次函数来表示．

滑行时间 $x/s$	0	1	2	3	$\dots$
滑行距离 $y/m$	0	4	12	24	$\dots$

（1）根据表中数据求出二次函数的表达式．现测量出滑雪者的出发点与终点的距离大约 $800m$，他需要多少时间才能到达终点？

（2）将得到的二次函数图象补充完整后，向左平移2个单位，再向上平移5个单位，求平移后的函数表达式．

某商店销售一款进价为每件40元的护肤品，调查发现，销售单价不低于40元且不高于80元时，该商品的日销售量 $y$（件 $)$与销售单价 $x$（元 $)$之间存在一次函数关系，当销售单价为44元时，日销售量为72件；当销售单价为48元时，日销售量为64件．

（1）求 $y$与 $x$之间的函数关系式；

（2）设该护肤品的日销售利润为 $w$（元 $)$，当销售单价 $x$为多少时，日销售利润 $w$最大，最大日销售利润是多少？