以初速度 (单位: 从地面竖直向上抛出小球,从抛出到落地的过程中,小球的高度 (单位: 与小球的运动时间 (单位: 之间的关系式是 .现将某弹性小球从地面竖直向上抛出,初速度为 ,经过时间 落回地面,运动过程中小球的最大高度为 (如图 ;小球落地后,竖直向上弹起,初速度为 ,经过时间 落回地面,运动过程中小球的最大高度为 (如图 .若 ,则 .
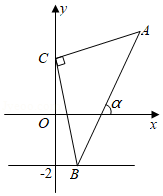
如图,已知点 ,点 为直线 上的一动点,点 , , 于点 ,连接 .若直线 与 正半轴所夹的锐角为 ,那么当 的值最大时, 的值为 .
某快餐店销售 、 两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份 种快餐的利润,同时提高每份 种快餐的利润.售卖时发现,在一定范围内,每份 种快餐利润每降1元可多卖2份,每份 种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是 元.
从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度 (单位: 与它距离喷头的水平距离 (单位: 之间满足函数关系式 喷出水珠的最大高度是 .

某快递公司在甲地和乙地之间共设有29个服务驿站(包括甲站、乙站),一辆快递货车由甲站出发,依次途经各站驶往乙站,每停靠一站,均要卸下前面各站发往该站的货包各1个,又要装上该站发往后面各站的货包各1个.在整个行程中,快递货车装载的货包数量最多是 个.
如图,已知 , 为线段 上的一个动点,分别以 , 为边在 的同侧作菱形 和菱形 ,点 , , 在一条直线上, . , 分别是对角线 , 的中点.当点 在线段 上移动时,点 , 之间的距离最短为 (结果留根号).

小明家的洗手盆上装有一种抬启式水龙头(如图 ,完全开启后,水流路线呈抛物线,把手端点 ,出水口 和落水点 恰好在同一直线上,点 至出水管 的距离为 ,洗手盆及水龙头的相关数据如图2所示,现用高 的圆柱型水杯去接水,若水流所在抛物线经过点 和杯子上底面中心 ,则点 到洗手盆内侧的距离 为 .

在一空旷场地上设计一落地为矩形 的小屋, ,拴住小狗的 长的绳子一端固定在 点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为 .
(1)如图1,若 ,则 .
(2)如图2,现考虑在(1)中的矩形 小屋的右侧以 为边拓展一正 区域,使之变成落地为五边形 的小屋,其他条件不变,则在 的变化过程中,当 取得最小值时,边 的长为 .

竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔1秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度,第一个小球抛出后 秒时在空中与第二个小球的离地高度相同,则 .
某农场拟建三间长方形种牛饲养室,饲养室的一面靠墙(墙长 ,中间用两道墙隔开(如图).已知计划中的建筑材料可建墙的总长度为 ,则这三间长方形种牛饲养室的总占地面积的最大值为 .

如图,在 中, , , ,以点 为原点建立平面直角坐标系,使 在 轴正半轴上,点 是 边上的一个动点, 交 于 , 于 , 于 .以下结论:
① ;
②当 为 的中点时, ;
③点 的坐标为 ;
④将 沿 所在的直线翻折到原来的平面,点 的对应点 的坐标为 ;
⑤矩形 的最大面积为3.在这些结论中正确的有 (只填序号)

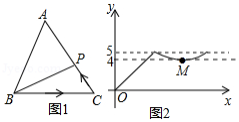
如图1,点 从 的顶点 出发,沿 匀速运动到点 ,图2是点 运动时,线段 的长度 随时间 变化的关系图象,其中 为曲线部分的最低点,则 的面积是 .
飞机着陆后滑行的距离 (单位: )关于滑行时间 (单位: )的函数解析式是 .在飞机着陆滑行中,最后 滑行的距离是 .
试题篮
()