某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元 件的商品售后,经过统计得到此商品单价在第
件的商品售后,经过统计得到此商品单价在第 天
天 为正整数)销售的相关信息,如表所示:
为正整数)销售的相关信息,如表所示:
销售量 |
|
销售单价 |
当 |
当 |
(1)请计算第几天该商品单价为25元 件?
件?
(2)求网店销售该商品30天里所获利润 (元
(元 关于
关于 (天
(天 的函数关系式;
的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?
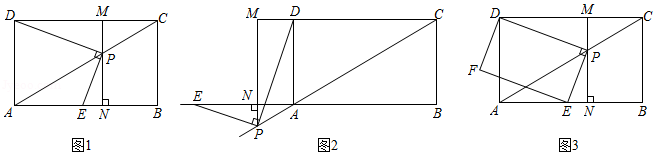
如图,矩形 中,点 为对角线 所在直线上的一个动点,连接 ,过点 作 ,交直线 于点 ,过点 作 ,交直线 于点 ,交直线 于点 . , .
(1)如图1,①当点 在线段 上时, 和 的数量关系为: ;
② 的值是 ;
(2)如图2,当点 在 延长线上时,(1)中的结论②是否成立?若成立,请证明;若不成立,说明理由;
(3)如图3,以线段 , 为邻边作矩形 .设 的长为 ,矩形 的面积为 .请直接写出 与 之间的函数关系式及 的最小值.
某商店销售一种销售成本为每件40元的玩具,若按每件50元销售,一个月可售出500件,销售价每涨1元,月销量就减少10件.设销售价为每件 元 ,月销量为 件,月销售利润为 元.
(1)写出 与 的函数解析式和 与 的函数解析式;
(2)商店要在月销售成本不超过10000的情况下,使月销售利润达到8000元,销售价应定为每件多少元?
(3)当销售价定为每件多少元时会获得最大利润?求出最大利润.
已知某厂以 小时 千克的速度匀速生产某种产品(生产条件要求 ,且每小时可获得利润 元.
(1)某人将每小时获得的利润设为 元,发现 时, ,所以得出结论:每小时获得的利润,最少是180元,他是依据什么得出该结论的,用你所学数学知识帮他进行解析说明;
(2)若以生产该产品2小时获得利润1800元的速度进行生产,则1天(按8小时计算)可生产该产品多少千克;
(3)要使生产680千克该产品获得的利润最大,问:该厂应该选取何种生产速度?并求此最大利润.
某水果店将标价为10元 斤的某种水果.经过两次降价后,价格为8.1元 斤,并且两次降价的百分率相同.
(1)求该水果每次降价的百分率;
(2)从第二次降价的第1天算起,第 天 为整数)的销量及储藏和损耗费用的相关信息如下表所示:
| 时间(天) |
|
| 销量(斤) |
|
| 储藏和损耗费用(元) |
|
已知该水果的进价为4.1元 斤,设销售该水果第 (天)的利润为 (元),求 与 之间的函数解析式,并求出第几天时销售利润最大,最大利润是多少?
如图,矩形 中,点 为对角线 所在直线上的一个动点,连接 ,过点 作 ,交直线 于点 ,过点 作 ,交直线 于点 ,交直线 于点 . , .
(1)如图1,①当点 在线段 上时, 和 的数量关系为: ;
② 的值是 ;
(2)如图2,当点 在 延长线上时,(1)中的结论②是否成立?若成立,请证明;若不成立,说明理由;
(3)如图3,以线段 , 为邻边作矩形 .设 的长为 ,矩形 的面积为 .请直接写出 与 之间的函数关系式及 的最小值.

小红经营的网店以销售文具为主,其中一款笔记本进价为每本10元,该网店在试销售期间发现,每周销售数量 (本 与销售单价 (元 之间满足一次函数关系,三对对应值如下表:
| 销售单价 (元 |
12 |
14 |
16 |
| 每周的销售量 (本 |
500 |
400 |
300 |
(1)求 与 之间的函数关系式;
(2)通过与其他网店对比,小红将这款笔记本的单价定为 元 ,且 为整数),设每周销售该款笔记本所获利润为 元,当销售单价定为多少元时每周所获利润最大,最大利润是多少元?
某超市销售一款"免洗洗手液",这款"免洗洗手液"的成本价为每瓶16元,当销售单价定为20元时,每天可售出80瓶.根据市场行情,现决定降价销售.市场调查反映:销售单价每降低0.5元,则每天可多售出20瓶(销售单价不低于成本价),若设这款"免洗洗手液"的销售单价为 (元 ,每天的销售量为 (瓶 .
(1)求每天的销售量 (瓶 与销售单价 (元 之间的函数关系式;
(2)当销售单价为多少元时,销售这款"免洗洗手液"每天的销售利润最大,最大利润为多少元?
如图,在平面直角坐标系中, 的顶点 是坐标原点,点 的坐标为 ,点 的坐标为 ,动点 从 开始以每秒1个单位长度的速度沿 轴正方向运动,设运动的时间为 秒 ,过点 作 轴,分别交 , 于点 , .
(1)填空: 的长为 , 的长为 ;
(2)当 时,求点 的坐标;
(3)请直接写出 的长为 (用含 的代数式表示);
(4)点 是线段 上一动点(点 不与点 , 重合), 和 的面积分别表示为 和 ,当 时,请直接写出 (即 与 的积)的最大值为 .

某服装厂生产 品种服装,每件成本为71元,零售商到此服装厂一次性批发 品牌服装 件时,批发单价为 元, 与 之间满足如图所示的函数关系,其中批发件数 为10的正整数倍.
(1)当 时, 与 的函数关系式为 .
(2)某零售商到此服装厂一次性批发 品牌服装200件,需要支付多少元?
(3)零售商到此服装厂一次性批发 品牌服装 件,服装厂的利润为 元,问: 为何值时, 最大?最大值是多少?

如图,四边形 是边长为1的正方形,点 是射线 上的动点(点 不与点 ,点 重合),点 在线段 的延长线上,且 ,连接 ,将 绕点 顺时针旋转 得到 ,连接 , , .设 ,四边形 的面积为 ,下列图象能正确反映出 与 的函数关系的是

| A. |
|
B. |
|
| C. |
|
D. |
|
某水果超市以每千克20元的价格购进一批樱桃,规定每千克樱桃售价不低于进价又不高于40元,经市场调查发现,樱桃的日销售量 (千克)与每千克售价 (元 满足一次函数关系,其部分对应数据如下表所示:
| 每千克售价 (元 |
|
25 |
30 |
35 |
|
| 日销售量 (千克) |
|
110 |
100 |
90 |
|
(1)求 与 之间的函数关系式;
(2)该超市要想获得1000的日销售利润,每千克樱桃的售价应定为多少元?
(3)当每千克樱桃的售价定为多少元时,日销售利润最大?最大利润是多少?
超市销售某品牌洗手液,进价为每瓶10元.在销售过程中发现,每天销售量 (瓶 与每瓶售价 (元 之间满足一次函数关系(其中 ,且 为整数),当每瓶洗手液的售价是12元时,每天销售量为90瓶;当每瓶洗手液的售价是14元时,每天销售量为80瓶.
(1)求 与 之间的函数关系式;
(2)设超市销售该品牌洗手液每天销售利润为 元,当每瓶洗手液的售价定为多少元时,超市销售该品牌洗手液每天销售利润最大,最大利润是多少元?
如图,在 中, , , 于点 .点 从点 出发,沿 的路径运动,运动到点 停止,过点 作 于点 ,作 于点 .设点 运动的路程为 ,四边形 的面积为 ,则能反映 与 之间函数关系的图象是

| A. |
|
B. |
|
| C. |
|
D. |
|
试题篮
()