在一副三角板ABC和DEF中,
(1)当AB∥CD,如图①。求∠DCB的度数。
(2)当CD与CB重合时,如图②,判定DE与AC的位置关系,并说明理由。
(3)如图③,当∠DCB等于多少度时,AB∥EC?


(年贵州省黔东南州)如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4=( )

| A.70° | B.80° | C.110° | D.100° |
(年贵州省黔南州)如图,下列说法错误的是( )
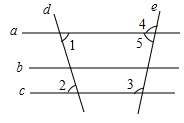
| A.若a∥b,b∥c,则a∥c |
| B.若∠1=∠2,则a∥c |
| C.若∠3=∠2,则b∥c |
| D.若∠3+∠5=180°,则a∥c |
(本题6分)如图,在△ABC中,点E在BC上,CD⊥AB, EF⊥AB,垂足分别为D、F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数.
(本题6分)AB⊥BC,∠1+∠2=90°,∠2=∠3.BE与DF平行吗?为什么?
解:BE∥DF.
∵AB⊥BC,
∴∠ABC= °,
即∠3+∠4= °.
又∵∠1+∠2=90°,
且∠2=∠3,
∴ = .
理由是:________________.
∴BE∥DF.
理由是:________________.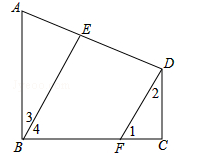
试题篮
()