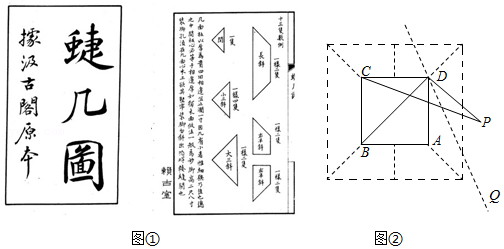
《蝶几图》是明朝人戈汕所作的一部组合家具的设计图
"  "为"蜨",同"蝶"
,它的基本组件为斜角形,包括长斜两只、右半斜两只、左半斜两只、闺一只、小三斜四只、大三斜两只,共十三只(图①中的"樣"和"隻"为"样"和"只"
.图②为某蝶几设计图,其中
和
为"大三斜"组件
"一樣二隻"的大三斜组件为两个全等的等腰直角三角形),已知某人位于点
处,点
与点
关于直线
对称,连接
、
.若
,则
度.
"为"蜨",同"蝶"
,它的基本组件为斜角形,包括长斜两只、右半斜两只、左半斜两只、闺一只、小三斜四只、大三斜两只,共十三只(图①中的"樣"和"隻"为"样"和"只"
.图②为某蝶几设计图,其中
和
为"大三斜"组件
"一樣二隻"的大三斜组件为两个全等的等腰直角三角形),已知某人位于点
处,点
与点
关于直线
对称,连接
、
.若
,则
度.
如图,在△ABC中,AB=BC,点E在边AB上,EF⊥AC于F.
(1)尺规作图:过点A作AD⊥BC于点D(保留作图痕迹,不写作法);
(2)求证:∠CAD=∠AEF;
(3)若∠ABC=45°,AD与EF交于点G,求证:EG=2AF.
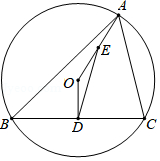
如图,已知锐角三角形内接于圆
,
于点
,连接
.
(1)若,
①求证:.
②当时,求
面积的最大值.
(2)点在线段
上,
,连接
,设
,
,
是正数),若
,求证:
.
如图是一张矩形纸片 ,点 是对角线 的中点,点 在 边上,把 沿直线 折叠,使点 落在对角线 上的点 处,连接 , .若 ,则 度.

发现规律
(1)如图①, 与 都是等边三角形,直线 , 交于点 .直线 , 交于点 .求 的度数.
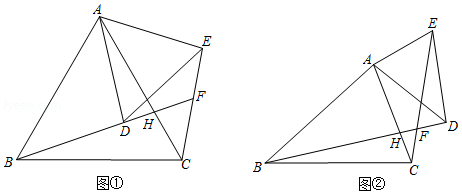
(2)已知: 与 的位置如图②所示,直线 , 交于点 .直线 , 交于点 .若 , ,求 的度数.
应用结论
(3)如图③,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 , 为 轴上一动点,连接 .将线段 绕点 逆时针旋转 得到线段 ,连接 , .求线段 长度的最小值.
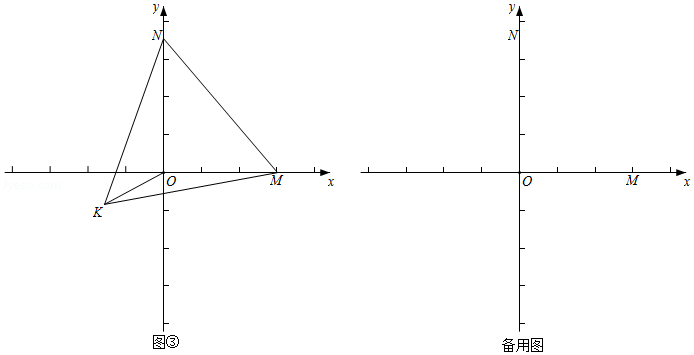
如图,在 中, , , , 于点 , 是 的中点,则 的长为

| A. |
1 |
B. |
2 |
C. |
3 |
D. |
4 |
如图,在 中, ,点 , 分别在边 , 上, ,连结 , .
(1)若 ,求 , 的度数;
(2)写出 与 之间的关系,并说明理由.

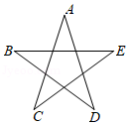
为庆祝中国共产党建党100周年,某校用红色灯带制作了一个如图所示的正五角星 , , , , 是正五角星的五个顶点),则图中 的度数是 度.
试题篮
()