如图, 中, , , 绕点 逆时针旋转 得到△ , 与 , 分别交于点 , .设 , 的面积为 ,则 与 的函数图象大致

A.
B.
C.
D.
如图,正方形 的边长为2,点 是 的中点, 与 交于点 , 是 上一点,连接 分别交 , 于点 , ,且 ,连接 ,则以下结论中:① ;② ;③ ;④ ,正确的是

A.①②③B.①②④C.①③④D.②③④
如图,在平行四边形 中, , ,过点 作边 的垂线 交 的延长线于点 ,点 是垂足,连接 、 , 交 于点 .则下列结论:①四边形 是正方形;② ;③ ;④ ,正确的个数是

A.1B.2C.3D.4
如图,正方形 中, 为 的中点, 的垂直平分线分别交 , 及 的延长线于点 , , ,连接 , , ,连接 并延长交 于点 .则下列结论中:
① ;② ;③ ;④ ;⑤
正确结论的个数有

A.2B.3C.4D.5
如图,正方形 中, , 为 的中点,将 沿 翻折得到 ,延长 交 于 , ,垂足为 ,连接 、 .以下结论:① ;② ;③ ;④ ;⑤ ;其中正确的个数是

A.2B.3C.4D.5
如图,在正方形 中, ,点 在 的边上,且 , 与 关于 所在的直线对称,将 按顺时针方向绕点 旋转 得到 ,连接 ,则线段 的长为

A.3B. C. D.
已知 ,求作 ,作法:
(1)以 为圆心,任意长为半径画弧分别交 , 于点 , ;
(2)分别以 , 为圆心,以 长为半径在角的内部画弧交于点 ;
(3)作射线 ,则 为 的平分线,可得
根据以上作法,某同学有以下3种证明思路:
①可证明 ,得 ,可得;
②可证明四边形 为菱形, , 互相垂直平分,得 ,可得;
③可证明 为等边三角形, , 互相垂直平分,从而得 ,可得.
你认为该同学以上3种证明思路中,正确的有

A.①②B.①③C.②③D.①②③
如图,正方形 的对角线相交于点 , 绕点 旋转,在旋转过程中,两个图形重叠部分的面积是正方形面积的

A. B. C. D.
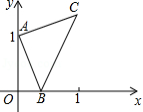
如图,点 的坐标为 ,点 是 轴正半轴上的一动点,以 为边作等腰直角 ,使 ,设点 的横坐标为 ,点 的纵坐标为 ,能表示 与 的函数关系的图象大致是
A. B.
B.
C. D.
D.
如图,在正方形 中, 为对角线, 为 上一点,过点 作 ,与 、 分别交于点 , , 为 的中点,连接 , , , .下列结论:
① ;② ;③ ;④若 ,则 ,其中结论正确的有

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
如图,在矩形 中, 的平分线与 交于 ,点 在 的延长线上, ,连接 、 , 与 交于 .有以下结论:
①
②
③
④
其中正确的个数是

A.1B.2C.3D.4
试题篮
()