初中数学全等三角形的应用试题

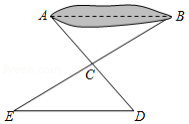
如图，有一池塘，要测池塘两端 $A$、 $B$的距离，可先在平地上取一个点 $C$，从点 $C$不经过池塘可以直接到达点 $A$和 $B$，连接 $\mathit{AC}$并延长到点 $D$，使 $\mathit{CD}=\mathit{CA}$，连接 $\mathit{BC}$并延长到点 $E$，使 $\mathit{CE}=\mathit{CB}$，连接 $\mathit{DE}$，那么量出 $\mathit{DE}$的长就是 $A$、 $B$的距离，为什么？请结合解题过程，完成本题的证明．

证明：在 $\mathit{\Delta DEC}$和 $\mathit{\Delta ABC}$中，

$\left\{\begin{array}{c}\mathit{CD}=(??)\\ (??)\\ \mathit{CE}=(??)\end{array}\right.$，

$\therefore \mathit{\Delta DEC}\cong \mathit{\Delta ABC}\left(\mathit{SAS}\right)$，

$\therefore$　 $\mathit{DE}=\mathit{AB}$　．

如图，有一池塘，要测池塘两端 $A$， $B$的距离，可先在平地上取一个点 $C$，从点 $C$不经过池塘可以直接到达点 $A$和 $B$．连接 $\mathit{AC}$并延长到点 $D$，使 $\mathit{CD}=\mathit{CA}$．连接 $\mathit{BC}$并延长到点 $E$，使 $\mathit{CE}=\mathit{CB}$．连接 $\mathit{DE}$，那么量出 $\mathit{DE}$的长就是 $A$， $B$的距离．为什么？

如图①，在 $\mathit{\Delta ABC}$中， $\angle \mathit{BAC}=90°$， $\mathit{AB}=\mathit{AC}$，点 $E$在 $\mathit{AC}$上（且不与点 $A$， $C$重合），在 $\mathit{\Delta ABC}$的外部作 $\mathit{\Delta CED}$，使 $\angle \mathit{CED}=90°$， $\mathit{DE}=\mathit{CE}$，连接 $\mathit{AD}$，分别以 $\mathit{AB}$， $\mathit{AD}$为邻边作平行四边形 $\mathit{ABFD}$，连接 $\mathit{AF}$．

（1）请直接写出线段 $\mathit{AF}$， $\mathit{AE}$的数量关系　　；

（2）将 $\mathit{\Delta CED}$绕点 $C$逆时针旋转，当点 $E$在线段 $\mathit{BC}$上时，如图②，连接 $\mathit{AE}$，请判断线段 $\mathit{AF}$， $\mathit{AE}$的数量关系，并证明你的结论；

（3）在图②的基础上，将 $\mathit{\Delta CED}$绕点 $C$继续逆时针旋转，请判断（2）问中的结论是否发生变化？若不变，结合图③写出证明过程；若变化，请说明理由．

人教版初中数学教科书八年级上册第48页告诉我们一种作已知角的平分线的方法：

已知：．

求作：的平分线．

作法：（1）以点为圆心，适当长为半径画弧，交于点，交于点．

（2）分别以点，为圆心，大于的长为半径画弧，两弧在的内部相交于点．

（3）画射线，射线即为所求（如图）．

请你根据提供的材料完成下面问题．

（1）这种作已知角的平分线的方法的依据是　　．（填序号）

①②③④

（2）请你证明为的平分线．

某校数学兴趣小组课外活动时，需要测量一个水塘的宽度，扎西设计了如下方案：如图所示，先在平地上取一点 $O$ ，从 $O$ 点不经过水塘可以直接到达水塘两端的点 $A$ 和点 $B$ ，连接 $\mathit{AO}$ 并延长到点 $C$ ，使 $\mathit{OC}=\mathit{OA}$ ，连接 $\mathit{BO}$ 并延长到点 $D$ ，使 $\mathit{OD}=\mathit{OB}$ ．测量出 $\mathit{CD}$ 的长就是水塘两端 $\mathit{AB}$ 的距离，扎西设计的方案正确吗？若正确请写出证明过程；若不正确请说明理由．