初中数学角平分线的性质试题

以 $\text{Rt}\Delta \text{ABC}$的锐角顶点 $A$为圆心，适当长为半径作弧，与边 $\mathit{AB}$， $\mathit{AC}$各相交于一点，再分别以这两个交点为圆心，适当长为半径作弧，过两弧的交点与点 $A$作直线，与边 $\mathit{BC}$交于点 $D$．若 $\angle \mathit{ADB}=60°$，点 $D$到 $\mathit{AC}$的距离为2，则 $\mathit{AB}$的长为　　．

如图，点 $D$是等边三角形 $\mathit{ABC}$外接圆上一点． $M$是 $\mathit{BD}$上一点，且满足 $\mathit{DM}=\mathit{DC}$，点 $E$是 $\mathit{AC}$与 $\mathit{BD}$的交点．

（1）求证： $\mathit{CM}//\mathit{AD}$；

（2）如果 $\mathit{AD}=1$， $\mathit{CM}=2$．求线段 $\mathit{BD}$的长及 $\mathit{\Delta BCE}$的面积．

已知：四边形 $\mathit{ABCD}$．

求作：点 $P$，使 $\angle \mathit{PCB}=\angle B$，且点 $P$到边 $\mathit{AD}$和 $\mathit{CD}$的距离相等．

如图，OP为∠AOB的平分线， $\mathit{PC}\perp \mathit{OB}$于点C，且 $\mathit{PC}＝3$，点P到OA的距离为　　．

如图，在 $x$轴， $y$轴上分别截取 $\mathit{OA}$， $\mathit{OB}$，使 $\mathit{OA}=\mathit{OB}$，再分别以点 $A$， $B$为圆心，以大于 $\frac{1}{2}\mathit{AB}$长为半径画弧，两弧交于点 $P$．若点 $P$的坐标为 $(a,2a-3)$，则 $a$的值为　　．

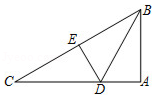
如图， BD是△ ABC的角平分线， DE是 BC的垂直平分线，∠ BAC＝90°， AD＝3，则 CD的长为（　　）

A．

3 $\sqrt{3}$

B．

6

C．

5

D．

4

如图，点 $P$为定角 $\angle \mathit{AOB}$的平分线上的一个定点，且 $\angle \mathit{MPN}$与 $\angle \mathit{AOB}$互补，若 $\angle \mathit{MPN}$在绕点 $P$旋转的过程中，其两边分别与 $\mathit{OA}$、 $\mathit{OB}$相交于 $M$、 $N$两点，则以下结论：（1） $\mathit{PM}=\mathit{PN}$恒成立；（2） $\mathit{OM}+\mathit{ON}$的值不变；（3）四边形 $\mathit{PMON}$的面积不变；（4） $\mathit{MN}$的长不变，其中正确的个数为 $($　　 $)$

A．4B．3C．2D．1

如图，在Rt△ ABC中，∠ B＝90°，以点 A为圆心，适当长为半径画弧，分别交 AB、 AC于点 D， E，再分别以点 D、 E为圆心，大于 $\frac{1}{2}$ DE为半径画弧，两弧交于点 F，作射线 AF交边 BC于点 G，若 BG＝1， AC＝4，则△ ACG的面积是（　　）

A．

1

B．

$\frac{3}{2}$

C．

2

D．

$\frac{5}{2}$

如图，已知 $\angle \mathit{AOB}=60°$，在 $\angle \mathit{AOB}$的平分线 $\mathit{OM}$上有一点 $C$，将一个 $120°$角的顶点与点 $C$重合，它的两条边分别与直线 $\mathit{OA}$、 $\mathit{OB}$相交于点 $D$、 $E$．

（1）当 $\angle \mathit{DCE}$绕点 $C$旋转到 $\mathit{CD}$与 $\mathit{OA}$垂直时（如图 $1)$，请猜想 $\mathit{OE}+\mathit{OD}$与 $\mathit{OC}$的数量关系，并说明理由；

（2）当 $\angle \mathit{DCE}$绕点 $C$旋转到 $\mathit{CD}$与 $\mathit{OA}$不垂直时，到达图2的位置，（1）中的结论是否成立？并说明理由；

（3）当 $\angle \mathit{DCE}$绕点 $C$旋转到 $\mathit{CD}$与 $\mathit{OA}$的反向延长线相交时，上述结论是否成立？请在图3中画出图形，若成立，请给于证明；若不成立，线段 $\mathit{OD}$、 $\mathit{OE}$与 $\mathit{OC}$之间又有怎样的数量关系？请写出你的猜想，不需证明．

如图，在 $\mathit{\Delta ABC}$中，点 $O$是角平分线 $\mathit{AD}$、 $\mathit{BE}$的交点，若 $\mathit{AB}=\mathit{AC}=10$， $\mathit{BC}=12$，则 $\tan \angle \mathit{OBD}$的值是 $($　　 $)$

A． $\frac{1}{2}$B．2C． $\frac{\sqrt{6}}{3}$D． $\frac{\sqrt{6}}{4}$

如图，已知锐角 $\mathit{\Delta ABC}$ 中， $\mathit{AC}=\mathit{BC}$ ．

（1）请在图1中用无刻度的直尺和圆规作图：作 $\angle \mathit{ACB}$ 的平分线 $\mathit{CD}$ ；作 $\mathit{\Delta ABC}$ 的外接圆 $\odot O$ ；（不写作法，保留作图痕迹）

（2）在（1）的条件下，若 $\mathit{AB}=\frac{48}{5}$ ， $\odot O$ 的半径为5，则 $\sin B=$ 　　．（如需画草图，请使用图 $2)$

如图，在 $\text{Rt}\Delta \text{ABC}$中， $\angle C=90°$， $\angle B=20°$， $\mathit{PQ}$垂直平分 $\mathit{AB}$，垂足为 $Q$，交 $\mathit{BC}$于点 $P$．按以下步骤作图：①以点 $A$为圆心，以适当的长为半径作弧，分别交边 $\mathit{AC}$， $\mathit{AB}$于点 $D$， $E$；②分别以点 $D$， $E$为圆心，以大于 $\frac{1}{2}\mathit{DE}$的长为半径作弧，两弧相交于点 $F$；③作射线 $\mathit{AF}$．若 $\mathit{AF}$与 $\mathit{PQ}$的夹角为 $\alpha$，则 $\alpha =$　    ．

如图，点 $P$是 $\angle \mathit{AOB}$平分线 $\mathit{OC}$上一点， $\mathit{PD}\perp \mathit{OB}$，垂足为 $D$，若 $\mathit{PD}=2$，则点 $P$到边 $\mathit{OA}$的距离是 $($　　 $)$

A．1B．2C． $\sqrt{3}$D．4

如图， $\mathit{OC}$为 $\angle \mathit{AOB}$的平分线， $\mathit{CM}\perp \mathit{OB}$， $\mathit{OC}=5$， $\mathit{OM}=4$，则点 $C$到射线 $\mathit{OA}$的距离为　　．

如图，在 $\text{Rt}\Delta \text{ABC}$中．

（1）利用尺规作图，在 $\mathit{BC}$边上求作一点 $P$，使得点 $P$到 $\mathit{AB}$的距离 $(\mathit{PD}$的长）等于 $\mathit{PC}$的长；

（2）利用尺规作图，作出（1）中的线段 $\mathit{PD}$．

（要求：尺规作图，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔描黑）