如图, 中, , ,点 , 分别在 , 上, ,点 为 的延长线与 的延长线的交点.
(1)求证: ;
(2)判断 和 的数量关系,并说明理由;
(3)若 , ,求 的长.

如图, 是 外接圆上的动点,且 , 位于 的两侧, ,垂足为 , 的延长线交此圆于点 . ,垂足为 , 交 于点 , , 的延长线交于点 ,且 .
(1)求证: ;
(2)设 外接圆的圆心为 ,若 , ,求 的大小.

中, , , ,过点 的直线把 分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是 .
有一张等腰三角形纸片, , ,小明将它沿虚线 剪开,得到 和四边形 两张纸片(如图所示),且满足 ,则下列五个数据 ,3, ,2, 中可以作为线段 长的有 个.

如图,在 中, ,以 为直径的 与边 , 分别交于 , 两点,过点 作 于点 .
(1)判断 与 的位置关系,并说明理由;
(2)求证: 为 的中点;
(3)若 , ,求 的长.

在矩形 中, , , 是对角线 上的动点,过点 作 于点 ,连接 ,当 是等腰三角形时, 的长为
A. B. C. 或 D. 或
如图,在 中, 平分 交 于点 ,过点 作 交 于点 ,且 平分 ,若 ,则 的长为

A.4B.6C. D.8
如图,在 中, 是 的中点,连接 并延长交 的延长线于点 .
(1)求证: ;
(2)连接 ,若 ,求证: .
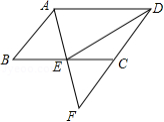
小明将两个直角三角形纸片如图(1)那样拼放在同一平面上,抽象出如图(2)的平面图形, 与 恰好为对顶角, ,连接 , ,点 是线段 上一点.
探究发现:
(1)当点 为线段 的中点时,连接 (如图(2) ,小明经过探究,得到结论: .你认为此结论是否成立? .(填"是"或"否"
拓展延伸:
(2)将(1)中的条件与结论互换,即: ,则点 为线段 的中点.请判断此结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.
问题解决:
(3)若 , ,求 的长.

如图,在 中, , , 的平分线交 于点 ,交 的延长线于点 , 于点 ,若 ,则 的周长为

A.16B.17C.24D.25
如图,在 中, , ,垂足为 , 平分 ,交 于点 ,交 于点 .若 , ,则 的长为
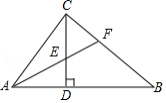
A. B. C. D.
试题篮
()