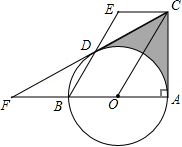
如图1,已知 是 的外接圆, 的平分线 交 于点 ,交 于点 ,连接 , .
(1)求证: ;
(2)如图2,在图1的基础上做 的直径 交 于点 ,连接 ,过点 做 的切线 ,若 ,求 的度数;
(3)在(2)的条件下,若 的面积为 , 与 的面积比为 ,求 的长.

如图,在 中,将 沿 折叠后,点 恰好落在 的延长线上的点 处.若 , ,则 的周长为

| A. |
12 |
B. |
15 |
C. |
18 |
D. |
21 |
如图, 是 的直径, ,四边形 是平行四边形, 交 于点 ,连接 并延长交 的延长线于点 .
(1)求证: 是 的切线;
(2)若 , ,求图中阴影部分的面积(结果保留根号和 ).
问题背景:我们学习等边三角形时得到直角三角形的一个性质:在直角三角形中,如果一个锐角等于 ,那么它所对的直角边等于斜边的一半.即:如图1,在 中, , ,则: .
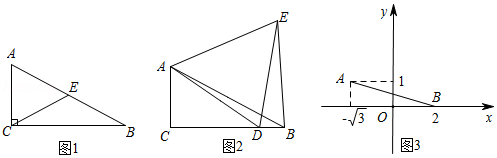
探究结论:小明同学对以上结论作了进一步研究.
(1)如图1,连接 边上中线 ,由于 ,易得结论:① 为等边三角形;② 与 之间的数量关系为 .
(2)如图2,点 是边 上任意一点,连接 ,作等边 ,且点 在 的内部,连接 .试探究线段 与 之间的数量关系,写出你的猜想并加以证明.
(3)当点 为边 延长线上任意一点时,在(2)条件的基础上,线段 与 之间存在怎样的数量关系?请直接写出你的结论 .
拓展应用:如图3,在平面直角坐标系 中,点 的坐标为 , ,点 是 轴正半轴上的一动点,以 为边作等边 ,当 点在第一象限内,且 时,求 点的坐标.
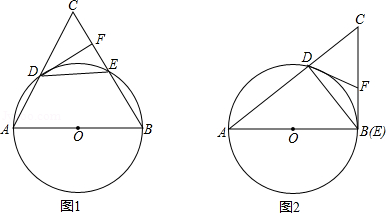
已知: 为 的直径, ,弦 ,直线 与 相交于点 ,弦 在 上运动且保持长度不变, 的切线 交 于点 .
(1)如图1,若 ,求证: ;
(2)如图2,当点 运动至与点 重合时,试判断 与 是否相等,并说明理由.
实验探究:
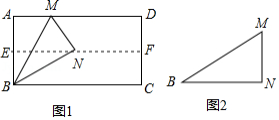
(1)如图1,对折矩形纸片 ,使 与 重合,得到折痕 ,把纸片展开;再一次折叠纸片,使点 落在 上,并使折痕经过点 ,得到折痕 ,同时得到线段 , .请你观察图1,猜想 的度数是多少,并证明你的结论.
(2)将图1中的三角形纸片 剪下,如图2.折叠该纸片,探究 与 的数量关系.写出折叠方案,并结合方案证明你的结论.
已知在菱形 中, ,对角线 、 相交于点 ,点 是线段 上一动点(不与点 , 重合),连接 ,以 为边在 的右侧作菱形 ,且 .
(1)如图1,若点 落在线段 上,请判断:线段 与线段 的数量关系是
(2)如图2,若点 不在线段 上,其它条件不变,(1)中的结论是否仍然成立?请给出判断并予以证明;
(3)若点
,
,
三点在同一直线上,其它条件不变,请直接写出线段
与线段
的数量关系.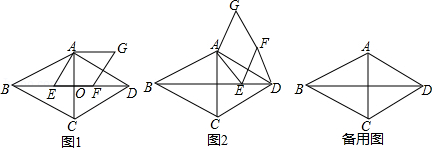
小颖在学习“两点之间线段最短”查阅资料时发现: 内总存在一点 与三个顶点的连线的夹角相等,此时该点到三个顶点的距离之和最小.
【特例】如图1,点 为等边 的中心,将 绕点 逆时针旋转 得到 ,从而有 ,连接 得到 ,同时 , ,即 、 、 、 四点共线,故 .在 中,另取一点 ,易知点 与三个顶点连线的夹角不相等,可证明 、 、 、 四点不共线,所以 ,即点 到三个顶点距离之和最小.

【探究】(1)如图2, 为 内一点, ,证明 的值最小;
【拓展】(2)如图3, 中, , , ,且点 为 内一点,求点 到三个顶点的距离之和的最小值.
如图,在菱形 中, ,点 、 分别是 、 上任意的点(不与端点重合),且 ,连接 与 相交于点 ,连接 与 相交于点 ,给出如下几个结论:
(1) ;
(2) 与 一定不垂直;
(3) 的大小为定值;
(4) ;
(5)若 ,则 .
其中正确结论的序号为 .
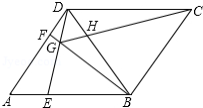
如图,点 是矩形 的边 上的点, ,将矩形沿着过点 的直线翻折后,点 、 分别落在边 下方的点 、 处,且点 、 、 在同一条直线上,折痕与边 交于点 , 与 交于点 .若 ,那么 的周长为

A. B. C. D.6
如图,在 中, , ,点 为 中点,点 为直线 上的动点(不与点 、点 重合),连接 、 ,将线段 绕点 顺时针旋转 ,得到线段 ,连接 .
(1)如图1,当点 在线段 上时,请直接写出线段 与 的数量关系.
(2)如图2,当点 在 延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;
(3)如图3,当点
在
延长线上时,若
,
,请求出
的长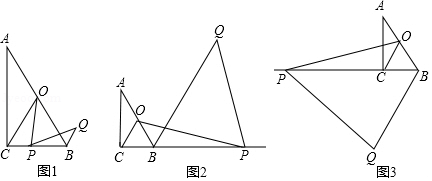
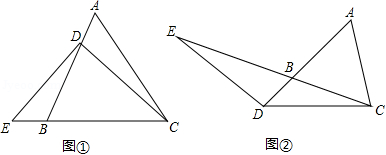
(1)已知: 是等腰三角形,其底边是 ,点 在线段 上, 是直线 上一点,且 ,若 (如图①).求证: ;
(2)若将(1)中的“点 在线段 上”改为“点 在线段 的延长线上”,其它条件不变(如图②),(1)的结论是否成立,并说明理由;
(3)若将(1)中的“若 ”改为“若 ”,其它条件不变,则 的值是多少?(直接写出结论,不要求写解答过程)
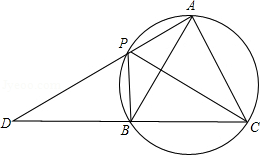
如图, , , , 是圆上的四个点, , , 的延长线相交于点 .
(1)求证: 是等边三角形;
(2)若 , ,求 的长.
试题篮
()