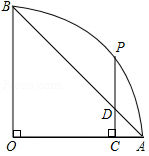
如图,扇形 中, . 为弧 上的一点,过点 作 ,垂足为 , 与 交于点 .若 , ,则该扇形的半径长为 .
如图,菱形 的对角线 , 交于点 , , ,将 沿点 到点 的方向平移,得到△ .当点 与点 重合时,点 与点 之间的距离为

A.6B.8C.10D.12
如图, 的半径 垂直于弦 ,垂足为点 ,连接 并延长交 于点 ,连接 , .若 , ,则 的面积为

A.12B.15C.16D.18
如图,在 中,半径 ,过点 的中点 作 交 于 、 两点,且 ,以 为圆心, 为半径作 ,交 于 点.
(1)求 的半径 的长;
(2)计算阴影部分的面积.

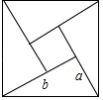
我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为 、 ,那么 的值是 .
如图,在 中, , , , 、 分别是斜边 、直角边 上的点,把 沿着直线 折叠.

(1)如图1,当折叠后点 和点 重合时,用直尺和圆规作出直线 ;(不写作法和证明,保留作图痕迹)
(2)如图2,当折叠后点 落在 边上点 处,且四边形 是菱形时,求折痕 的长.
中, , , ,过点 的直线把 分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是 .
在四边形 中, , , , .以 为腰作等腰 ,使 ,过点 作 交直线 于点 .请画出图形,并直接写出 的长.
如图,正方形 中, 为 的中点, 的垂直平分线分别交 , 及 的延长线于点 , , ,连接 , , ,连接 并延长交 于点 .则下列结论中:
① ;② ;③ ;④ ;⑤
正确结论的个数有

A.2B.3C.4D.5
如图,方格纸中每个小正方形的边长均为1,线段 的两个端点均在小正方形的顶点上.
(1)在图中画出以线段 为一边的矩形 (不是正方形),且点 和点 均在小正方形的顶点上;
(2)在图中画出以线段 为一腰,底边长为 的等腰三角形 ,点 在小正方形的顶点上,连接 ,请直接写出线段 的长.

如图, 是 内一点, , , , , 、 、 、 分别是 、 、 、 的中点,则四边形 的周长为
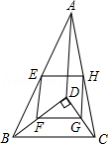
A.12B.14C.24D.21
试题篮
()