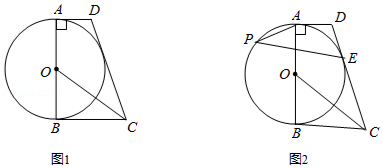
如图1,在四边形 中, , , 是 的直径, 平分 .
(1)求证:直线 与 相切;
(2)如图2,记(1)中的切点为 , 为优弧 上一点, , .求 的值.
如图,点是线段
上一点,
,以点
为圆心,
的长为半径作
,过点
作
的垂线交
于
,
两点,点
在线段
的延长线上,连接
交
于点
,以
,
为边作
.
(1)求证:是
的切线;
(2)若,求四边形
与
重叠部分的面积;
(3)若,
,连接
,求
和
的长.

如图,已知正方形的边长为
,
为
边上一点(不与端点重合),将
沿
对折至
,延长
交边
于点
,连接
,
.
给出下列判断:
①;
②若,则
;
③若为
的中点,则
的面积为
;
④若,则
;
⑤.
其中正确的是 .(写出所有正确判断的序号)

如图①,已知正方体的棱长为
,
,
,
分别是
,
,
的中点,截面
将这个正方体切去一个角后得到一个新的几何体(如图②
,则图②中阴影部分的面积为
.

如图,矩形中,
,
,点
是对角线
的中点,过点
的直线分别交
、
边于点
、
.
(1)求证:四边形是平行四边形;
(2)当时,求
的长.

如图,正方形 ,点 , 分别在 , 上,且 , 与 相交于点 .
(1)求证: ;
(2)若 , ,求 的长.

如图,在平面直角坐标系中,菱形的顶点
为坐标原点,顶点
在
轴的正半轴上,顶点
在反比例函数
的图象上,已知菱形的周长是8,
,则
的值是 .

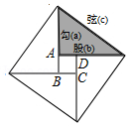
公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾,弦
,则小正方形
的面积是 .
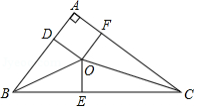
我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知 , , ,则正方形 的边长是
| A. |
|
B. |
2 |
C. |
|
D. |
4 |
试题篮
()