初中数学勾股定理解答题

如图，在矩形中，，，为边上一点，，连接．动点、从点同时出发，点以的速度沿向终点运动；点以的速度沿折线向终点运动．设点运动的时间为，在运动过程中，点，点经过的路线与线段围成的图形面积为．

（1）　　，　　；

（2）求关于的函数解析式，并写出自变量的取值范围；

（3）当时，直接写出的值．

如图，在中，，，．点从点出发，沿向终点运动，同时点从点出发，沿射线运动，它们的速度均为每秒5个单位长度，点到达终点时，、同时停止运动．当点不与点、重合时，过点作于点，连结，以、为邻边作．设与重叠部分图形的面积为，点的运动时间为秒．

（1）①的长为　　；

②的长用含的代数式表示为　　．

（2）当为矩形时，求的值；

（3）当与重叠部分图形为四边形时，求与之间的函数关系式；

（4）当过点且平行于的直线经过一边中点时，直接写出的值．

如图，在四边形中，，，对角线，交于点，平分，过点作交的延长线于点，连接．

（1）求证：四边形是菱形；

（2）若，，求的长．

如图，是的一条弦，是的中点，过点作于点，过点作的切线交的延长线于点．

（1）求证：；

（2）若，，求的半径．

如图，在四边形 $\mathit{ABCD}$ 中， $\angle \mathit{ABC}=90°$ ， $\mathit{AC}=\mathit{AD}$ ， $M$ ， $N$ 分别为 $\mathit{AC}$ ， $\mathit{CD}$ 的中点，连接 $\mathit{BM}$ ， $\mathit{MN}$ ， $\mathit{BN}$ ．

（1）求证： $\mathit{BM}=\mathit{MN}$ ；

（2） $\angle \mathit{BAD}=60°$ ， $\mathit{AC}$ 平分 $\angle \mathit{BAD}$ ， $\mathit{AC}=2$ ，求 $\mathit{BN}$ 的长．

在中，，，是的中点．为直线上一动点，连接．过点作，交直线于点，连接．

（1）如图1，当是线段的中点时，设，，求的长（用含，的式子表示）；

（2）当点在线段的延长线上时，依题意补全图2，用等式表示线段，，之间的数量关系，并证明．

如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B

（1）求证：△ADF∽△DEC；
（2）若AB=8，AD=6，AF=4，求AE的长．

小薇将一副三角尺如图所示摆放在一起，发现只要知道其中一边的长就可以求出其他各边的长，若已知=，求的长．

如图，P为等腰△ABC的顶角A的外角平分线上任一点，连接PB，PC．

（1）求证：PB+PC＞2AB．
（2）当PC=2，PB=，∠ACP=45°时，求AB的长．

（年贵州省毕节）如图，以△ABC的BC边上一点O为圆心的圆，经过A，B两点，且与BC边交于点E，D为BE的下半圆弧的中点，连接AD交BC于F，AC=FC．

（1）求证：AC是⊙O的切线；
（2）已知圆的半径R=5，EF=3，求DF的长．

（年云南省昆明市）如图，AH是⊙O的直径，AE平分∠FAH，交⊙O于点E，过点E的直线FG⊥AF，垂足为F，B为直径OH上一点，点E、F分别在矩形ABCD的边BC和CD上．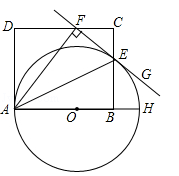

（1）求证：直线FG是⊙O的切线；
（2）若CD=10，EB=5，求⊙O的直径．

（年青海省中考）如图，在△ABC中，∠B=60°，⊙O是△ABC的外接圆，过点A作⊙O的切线，交CO的延长线于点M，CM交⊙O于点D．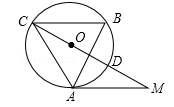

（1）求证：AM=AC；
（2）若AC=3，求MC的长．

（年新疆乌鲁木齐市）如图，AB是⊙O的直径，CD与⊙O相切于点C，与AB的延长线交于点D，DE⊥AD且与AC的延长线交于点E．

（1）求证：DC=DE；
（2）若tan∠CAB=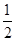，AB=3，求BD的长．

（年贵州省遵义市）如图，△ABC中，AB=AC，以AB为直径作⊙O，交BC于点D，交CA的延长线于点E，连接AD、DE．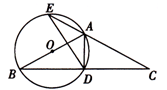

（1）求证：D是BC的中点；
（2）若DE=3，BD—AD=2，求⊙O的半径；
（3）在（2）的条件下，求弦AE的长．

（年贵州省贵阳市）如图，在矩形纸片ABCD中，AB=4，AD=12，将矩形纸片折叠，使点C落在AD边上的点M处，折痕为PE，此时PD=3．

（1）求MP的值；
（2）在AB边上有一个动点F，且不与点A，B重合．当AF等于多少时，△MEF的周长最小？
（3）若点G，Q是AB边上的两个动点，且不与点A，B重合，GQ=2．当四边形MEQG的周长最小时，求最小周长值．（计算结果保留根号）