研究立体图形问题的基本思路是把立体图形问题转化为平面图形问题.
(1)阅读材料
立体图形中既不相交也不平行的两条直线所成的角,就是将直线平移使其相交所成的角.
例如,正方体 (图 ,因为在平面 中, , 与 相交于点 ,所以直线 与 所成的 就是既不相交也不平行的两条直线 与 所成的角.
解决问题
如图1,已知正方体 ,求既不相交也不平行的两直线 与 所成角的大小.

(2)如图2, , 是正方体相邻两个面上的点;
①下列甲、乙、丙三个图形中,只有一个图形可以作为图2的展开图,这个图形是 ;
②在所选正确展开图中,若点 到 , 的距离分别是2和5,点 到 , 的距离分别是4和3, 是 上一动点,求 的最小值.

在几何体表面上,蚂蚁怎样爬行路径最短?
(1)如图①,圆锥的母线长为 , 为母线 的中点,点 在底面圆周上, 的长为 .在图②所示的圆锥的侧面展开图中画出蚂蚁从点 爬行到点 的最短路径,并标出它的长(结果保留根号).

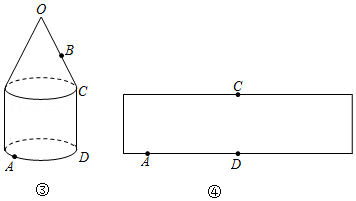
(2)图③中的几何体由底面半径相同的圆锥和圆柱组成. 是圆锥的顶点,点 在圆柱的底面圆周上,设圆锥的母线长为 ,圆柱的高为 .
①蚂蚁从点 爬行到点 的最短路径的长为 (用含 , 的代数式表示).
②设 的长为 ,点 在母线 上, .圆柱的侧面展开图如图④所示,在图中画出蚂蚁从点 爬行到点 的最短路径的示意图,并写出求最短路径的长的思路.
如图,圆柱形玻璃杯高为 ,底面周长为 ,在杯内壁离杯底 的点 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿 与蜂蜜相对的点 处,则蚂蚁从外壁 处到内壁 处的最短距离为 (杯壁厚度不计).

如图,已知圆柱的底面直径 ,高 ,小虫在圆柱表面爬行,从 点爬到 点,然后再沿另一面爬回 点,则小虫爬行的最短路程为

A. B. C. D.
如图所示,圆柱的高 ,底面直径 ,现在有一只蚂蚁想要从 处沿圆柱表面爬到对角 处捕食,则它爬行的最短距离是

A. B. C. D.
圆锥的底面周长为 ,母线长为2,点 是母线 的中点,一根细绳(无弹性)从点 绕圆锥侧面一周回到点 ,则细绳的最短长度为 .
我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点 处缠绕而上,绕五周后其末端恰好到达点 处,则问题中葛藤的最短长度是 尺.

试题篮
()