在综合实践课上,老师要求同学用正方形纸片剪出正三角形且正三角形的顶点都在正方形边上.小红利用两张边长为2的正方形纸片,按要求剪出了一个面积最大的正三角形和一个面积最小的正三角形.则这两个正三角形的边长分别是 .
△ABC为等边三角形, , 于点D,E为线段 上一点, .以AE为边在直线 右侧构造等边三角形 ,连接 ,N为 的中点.
(1)如图1, 交于点G,连接 ,求线段 的长;
(2)如图2,将 绕点A逆时针旋转,旋转角为α,M为线段EF的中点,连接 , .当 时,猜想∠DNM的大小是否为定值,并证明你的结论;
(3)连接BN,在 绕点A逆时针旋转过程中,当线段BN最大时,请直接写出 的面积.

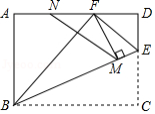
如图,矩形纸片 , , , 为边 上一点.将 沿 所在的直线折叠,点 恰好落在 边上的点 处,过点 作 ,垂足为点 ,取 的中点 ,连接 ,则 .
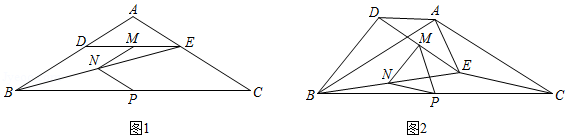
如图,点 为 的重心,连接 , 并延长分别交 , 于点 , ,连接 ,若 , , ,则 的长度为

A.1.7B.1.8C.2.2D.2.4
如图,点 , 的坐标分别为 , ,点 为坐标平面内一点, ,点 为线段 的中点,连接 ,则 的最大值为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,菱形 的边长为1, ,点 是边 上任意一点(端点除外),线段 的垂直平分线交 , 分别于点 , , , 的中点分别为 , .
(1)求证: ;
(2)求 的最小值;
(3)当点 在 上运动时, 的大小是否变化?为什么?
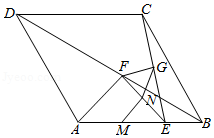
如图1,在等腰三角形 中, , ,点 、 分别在边 、 上, ,连接 ,点 、 、 分别为 、 、 的中点.
(1)观察猜想.
图1中,线段 、 的数量关系是 , 的大小为 .
(2)探究证明
把 绕点 顺时针方向旋转到如图2所示的位置,连接 、 、 ,判断 的形状,并说明理由;
(3)拓展延伸
把 绕点 在平面内自由旋转,若 , ,请求出 面积的最大值.
如图,在 中, , 为中线,延长 至点 ,使 ,连结 , 为 中点,连结 .若 , ,则 的长为

A.2B.2.5C.3D.4
如图,在 中, , 是 的中点,过点 作 的平行线交 于点 ,作 的垂线交 于点 ,若 ,且 的面积为1,则 的长为

A. B.5C. D.10
如图,点 的坐标是 , ,点 是以 为直径的 上一动点,点 关于点 的对称点为 .当点 在 上运动时,所有这样的点 组成的图形与直线 有且只有一个公共点,则 的值等于 .

如图,菱形 的对角线 、 相交于点 ,点 为边 的中点,若菱形 的周长为16, ,则 的面积是

A. B.2C. D.4
如图,在 中,延长 至 ,使得 ,过 中点 作 (点 位于点 右侧),且 ,连接 .若 ,则 的长为

A.3B.4C. D.
试题篮
()