如图, 内接于 , 为 的直径, 是 的切线, 为切点, ,垂足为 ,交 于 ,连接 .
(1)求证: 平分 ;
(2)若 的半径为1, ,求 及 的长.

如图,在正方形 中,对角线 与 相交于点 , 为 上一点, , 为 的中点.若 的周长为18,则 的长为 .

如图, 为等腰三角形, , 为 内一点,连接 ,将线段 绕点 旋转至 ,使得 , , , 分别为 , , 的中点,连接 , , , .
(1)求证: ;
(2)试说明 与 互补.
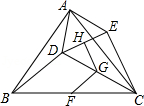
如图, 为等腰三角形, , 为 内一点,连接 ,将线段 绕点 旋转至 ,使得 , , , 分别为 , , 的中点,连接 , , , .
(1)求证: ;
(2)试说明 与 互补.
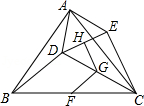
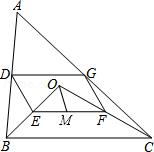
如图,点 是 内一点,连接 、 ,并将 、 、 、 的中点 、 、 、 依次连接,得到四边形 .
(1)求证:四边形 是平行四边形;
(2)若 为 的中点, , 和 互余,求 的长度.
如图, 是 的直径, , 是 上的点,且 , 分别与 , 相交于点 , ,则下列结论:
① ;② ;③ 平分 ;④ ;⑤ ;⑥ ,其中一定成立的是

A.②④⑤⑥B.①③⑤⑥C.②③④⑥D.①③④⑤
如图,在 中, , 于点 , 是 上一点,以 为直径的 交 于点 ,连接 ,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.

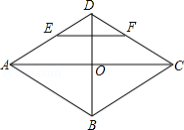
菱形 的对角线 , 相交于点 , , 分别是 , 边上的中点,连接 .若 , ,则菱形 的面积为
| A. |
|
B. |
|
C. |
|
D. |
|
(探索发现)
如图①,是一张直角三角形纸片, ,小明想从中剪出一个以 为内角且面积最大的矩形,经过多次操作发现,当沿着中位线 、 剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .
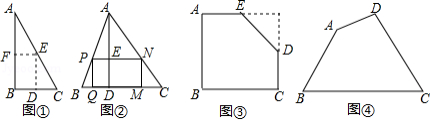
(拓展应用)
如图②,在 中, , 边上的高 ,矩形 的顶点 、 分别在边 、 上,顶点 、 在边 上,则矩形 面积的最大值为 .(用含 , 的代数式表示)
(灵活应用)
如图③,有一块“缺角矩形” , , , , ,小明从中剪出了一个面积最大的矩形( 为所剪出矩形的内角),求该矩形的面积.
(实际应用)
如图④,现有一块四边形的木板余料 ,经测量 , , ,且 ,木匠徐师傅从这块余料中裁出了顶点 、 在边 上且面积最大的矩形 ,求该矩形的面积.
试题篮
()