如图,已知 是 的直径,半径 ,点 在劣弧 上(不与点 ,点 重合), 与 交于点 .设 , ,则

A. B. C. D.
小亮在学习中遇到这样一个问题:
如图,点 是 上一动点,线段 ,点 是线段 的中点,过点 作 ,交 的延长线于点 .当 为等腰三角形时,求线段 的长度.
小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题.请将下面的探究过程补充完整:
(1)根据点 在 上的不同位置,画出相应的图形,测量线段 , , 的长度,得到下表的几组对应值.
|
0 |
1.0 |
2.0 |
3.0 |
4.0 |
5.0 |
6.0 |
7.0 |
8.0 |
|
8.0 |
7.7 |
7.2 |
6.6 |
5.9 |
|
3.9 |
2.4 |
0 |
|
8.0 |
7.4 |
6.9 |
6.5 |
6.1 |
6.0 |
6.2 |
6.7 |
8.0 |
操作中发现:
①“当点 为 的中点时, ”.则上表中 的值是 5.0 ;
②“线段 的长度无需测量即可得到”.请简要说明理由.
(2)将线段 的长度作为自变量 , 和 的长度都是 的函数,分别记为 和 ,并在平面直角坐标系 中画出了函数 的图象,如图所示.请在同一坐标系中画出函数 的图象;
(3)继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当 为等腰三角形时,线段 长度的近似值(结果保留一位小数).


如图,一次函数 与反比例函数 的图象交于 , 两点,点 在以 为圆心,1为半径的 上, 是 的中点,已知 长的最大值为 ,则 的值为

A. B. C. D.
如图,已知 是 的直径,点 在圆周上(不与 、 重合),点 在 的延长线上,连接 交 于点 ,若 ,则
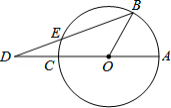
A. B. C. D.
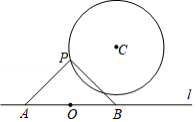
如图,已知 的半径为3,圆外一定点 满足 ,点 为 上一动点,经过点 的直线 上有两点 、 ,且 , , 不经过点 ,则 的最小值为 .
如图, 是半圆 的直径, 是 延长线上的点, 的垂直平分线交半圆于点 ,交 于点 ,连接 , .已知半圆 的半径为3, .
(1)求 的长.
(2)点 是线段 上一动点,连接 ,作 , 交线段 于点 .当 为等腰三角形时,求 的长.

对下列生活现象的解释其数学原理运用错误的是( )
A.把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理
B.木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“直线外一点与直线上各点连接的所有线段中,垂线段最短”的原理
C.将自行车的车架设计为三角形形状是运用了“三角形的稳定性”的原理
D.将车轮设计为圆形是运用了“圆的旋转对称性”的原理
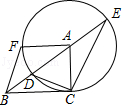
如图,在Rt△ ACB中,∠ ACB=90°,以点 A为圆心, AC长为半径的圆交 AB于点 D, BA的延长线交⊙ A于点 E,连接 CE, CD, F是⊙ A上一点,点 F与点 C位于 BE两侧,且∠ FAB=∠ ABC,连接 BF.
(1)求证:∠ BCD=∠ BEC;
(2)若 BC=2, BD=1,求 CE的长及sin∠ ABF的值.
如图,在等边 中, ,点 , 分别在边 , 上,且 ,连接 , 交于点 ,连接 ,则 的最小值是 .

如图,在 中, ,点 为 边上一点,以点 为圆心, 长为半径的圆与边 相交于点 ,连接 ,当 为 的切线时.
(1)求证: ;
(2)若 , 的半径为1,请直接写出 的长为 .

(1)如图①,点 在 上,点 在 上, , .求证: .
(2)如图②, 为 上一点,按以下步骤作图:
①连接 ;
②以点 为圆心, 长为半径作弧,交 于点 ;
③在射线 上截取 ;
④连接 .
若 ,求 的半径.

试题篮
()