如图,在 中, , .以 为直径的 交 于点 . 是 上一点,且 ,连接 .过点 作 ,交 的延长线于点 ,则 的度数为

A. B. C. D.
问题背景:
如图①,在四边形 中, , ,探究线段 , , 之间的数量关系.
小吴同学探究此问题的思路是:将 绕点 ,逆时针旋转 到 处,点 , 分别落在点 , 处(如图② ,易证点 , , 在同一条直线上,并且 是等腰直角三角形,所以 ,从而得出结论: .
简单应用:
(1)在图①中,若 , ,则 .
(2)如图③, 是 的直径,点 、 在 上, ,若 , ,求 的长.
拓展规律:
(3)如图④, , ,若 , ,求 的长(用含 , 的代数式表示)
(4)如图⑤, , ,点 为 的中点,若点 满足 , ,点 为 的中点,则线段 与 的数量关系是 .
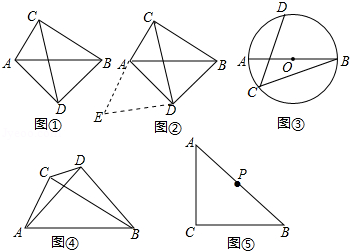
如图, 是 的直径,点 和点 是 上的两点,过点 作 的切线交 延长线于点 .
(1)若 ,求 的度数;
(2)若 , ,求 半径的长.
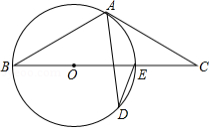
如图,已知 为 直径, 是 的中点, 交 的延长线于 , 的切线交 的延长线于 .
(1)求证:直线 与 相切;
(2)已知 且 , 的半径为5,求 的值.
如图,在 中, 为直径, 、 为圆上两点, 为圆外一点,且 .
(1)求证: 为 的切线.
(2)若 , ,求 的半径.

如图, 是 的直径,弦 与 相交于点 , 与 相切于点 ,交 的延长线于点 , , , .
(1)求 的度数;
(2)求 的长度.

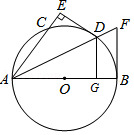
如图,五边形 内接于 , 与 相切于点 ,交 延长线于点 .
(1)若 , ,求证: ;
(2)若 , , ,求 的长.
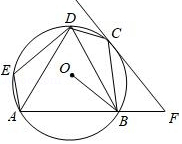
如图, , , , 是 上的四个点, 是 的中点, 是半径 上任意一点.若 ,则 的度数不可能是
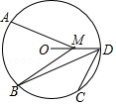
A. B. C. D.
试题篮
()