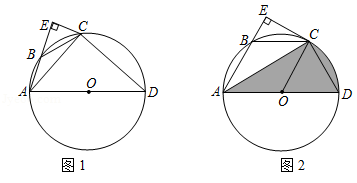
如图1,四边形 内接于 , 为直径,点 作 于点 ,连接 .
(1)求证: ;
(2)若 是 的切线, ,连接 ,如图2.
①请判断四边形 的形状,并说明理由;
②当 时,求 , 与 围成阴影部分的面积.
在一次数学探究活动中,李老师设计了一份活动单:
已知线段 ,使用作图工具作 ,尝试操作后思考: (1)这样的点 唯一吗? (2)点 的位置有什么特征?你有什么感悟? |
“追梦”学习小组通过操作、观察、讨论后汇报:点 的位置不唯一,它在以 为弦的圆弧上(点 、 除外), .小华同学画出了符合要求的一条圆弧(如图 .
(1)小华同学提出了下列问题,请你帮助解决.
①该弧所在圆的半径长为 ;
② 面积的最大值为 ;
(2)经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图1所示的弓形内部,我们记为 ,请你根据图1证明 .
(3)请你运用所学知识,结合以上活动经验,解决问题:如图2,已知矩形 的边长 , ,点 在直线 的左侧,且 .
①线段 长的最小值为 ;
②若 ,则线段 长为 .

如图1, 是 的直径,点 是 上一动点,且不与 , 两点重合, 的平分线交 于点 ,过点 作 ,交 的延长线于点 .

(1)求证: 是 的切线;
(2)求证: ;
(3)如图2,原有条件不变,连接 , ,延长 至点 , 的平分线交 的延长线于点 , 的平分线交 的平分线于点 .求证:无论点 如何运动,总有 .
如图,在 中, ,点 在 边上,过 , , 三点的 交 边于另一点 ,且 是 的中点, 是 的一条直径,连接 并延长交 边于 点.
(1)求证:四边形 为平行四边形;
(2)当 时,求 的值.

如图, 、 是 的切线, 、 是切点, 是 的直径,连接 ,交 于点 ,交 于点 .
(1)求证: ;
(2)若 恰好是 的中点,且四边形 的面积是 ,求阴影部分的面积;
(3)若 ,且 ,求切线 的长.

如图,在 中, ,以 为直径的 与 相交于点 , ,垂足为 .
(1)求证: 是 的切线;
(2)若弦 垂直于 ,垂足为 , , ,求 的半径;
(3)在(2)的条件下,当 时,求线段 的长.

如图,已知 内接于 , 是 的直径, 的平分线交 于点 ,交 于点 ,连接 ,作 ,交 的延长线于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径和 的长.

如图,在 中, 为 的直径, 为 的弦,点 是 的中点,过点 作 的垂线,交 于点 ,交 于点 ,分别连接 , .
(1) 与 的数量关系是 ;
(2)求证: ;
(3)若 , ,求阴影部分图形的面积.

如图,在 中, , 是 上的一点,以 为直径的 与 相切于点 ,连接 , .
(1)求证: 平分 ;
(2)若 ,求 的值.

如图, 内接于 , 是 的直径 的延长线上一点, .过圆心 作 的平行线交 的延长线于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径及 的值.

如图, 是 的外接圆, 是 的直径, 于点 .
(1)求证: ;
(2)连接 并延长,交 于点 ,交 于点 ,连接 .若 的半径为5, ,求 和 的长.

定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.
(1)如图1, 是 中 的遥望角,若 ,请用含 的代数式表示 .
(2)如图2,四边形 内接于 , ,四边形 的外角平分线 交 于点 ,连结 并延长交 的延长线于点 .求证: 是 中 的遥望角.
(3)如图3,在(2)的条件下,连结 , ,若 是 的直径.
①求 的度数;
②若 , ,求 的面积.

如图,已知 , 为 的两条直径,连接 , , 于点 ,点 是半径 的中点,连接 .
(1)设 的半径为1,若 ,求线段 的长.
(2)连接 , ,设 与 交于点 ,
①求证: .
②若 ,求 的度数.

问题提出
(1)如图1,在 中, , , 的平分线交 于点 .过点 分别作 , .垂足分别为 , ,则图1中与线段 相等的线段是 .
问题探究
(2)如图2, 是半圆 的直径, . 是 上一点,且 ,连接 , . 的平分线交 于点 ,过点 分别作 , ,垂足分别为 , ,求线段 的长.
问题解决
(3)如图3,是某公园内“少儿活动中心”的设计示意图.已知 的直径 ,点 在 上,且 . 为 上一点,连接 并延长,交 于点 .连接 , .过点 分别作 , ,垂足分别为 , .按设计要求,四边形 内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设 的长为 ,阴影部分的面积为 .
①求 与 之间的函数关系式;
②按照“少儿活动中心”的设计要求,发现当 的长度为 时,整体布局比较合理.试求当 时.室内活动区(四边形 的面积.

试题篮
()