初中数学圆内接四边形的性质选择题

如图，图1、图2、图3分别表示甲、乙、丙三人由A地到B地的路线图（箭头表示行进的方向）．其中E为AB的中点，AH＞HB，判断三人行进路线长度的大小关系为（     ）

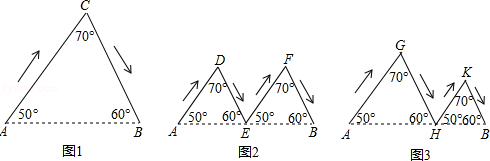
A．甲＜乙＜丙

B．乙＜丙＜甲

C．丙＜乙＜甲

D．甲=乙=丙

如图，四边形ABCD和四边形AEFC是两个矩形，点B在EF边上，若矩形ABCD和矩形AEFC的面积分别是S₁、S₂的大小关系是（           ）

A．S1＞S2

B．S1=S2

C．S1＜S2

D．3S1=2S2

下列个命题中，是真命题的是（   ）

A．若x＞y，则x^2＞y^2

B．若（x1，y1）、（x2，y2）是函数图象上的两点，且x1＜x2，则y1＞y2

C．有两角及一边对应相等的两个三角形全等

D．对角线互相垂直的平行四边形是正方形

四边形ABCD的对角线AC和BD相交于点O，设有下列条件：①AB=AD；②∠DAB=90°；③AO=CO，BO=DO；④矩形ABCD；⑤菱形ABCD，⑥正方形ABCD，则下列推理不成立的是（    ）

A．①④→⑥

B．①③→⑤

C．①②→⑥

D．②③→④

如图，点P是矩形ABCD的边AD上的一个动点，矩形的两条边AB、BC的长分别为3和4，那么点P到矩形的两条对角线AC、BD的距离之和是（  ）

A．            B．      C．           D．不确定

如图，在菱形ABCD中，AE⊥BC于点E，AF⊥CD于点F，且E、F分别为BC、CD的中点，则∠EAF等于（  ）

A．75°    B．60°      C．45°     D．30°

如图，在正方形ABCD中，对角线BD的长为．若将BD绕点B旋转后，点D落在BC延长线上的点D′处，点D经过的路径为，则图中阴影部分的面积是（ ）

A．﹣1	B．﹣
C．﹣	D．π﹣2

如图，在正方形ABCD中，AC、BD相交于点O，把△ABC折叠，使AB落在AC上，点B与AC上的点E重合，展开后，折痕AG交BD于点F，连结EG、EF．下列结论：①tan∠AGB=2；②图中有9对全等三角形；③若将△GEF沿EF折叠，则点G不一定落在AC上；④BG=BF；⑤S_{四边形GFOE}=S_△AOF，上述结论中正确的个数是（ ）

A．1个       B．2个       C．3个       D．4个

如图，已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm，AE⊥BC于点E，则AE的长是（ ）

A．cm       B．cm       C．cm       D．cm

如图．矩形纸片ABCD中，已知AD=8，折叠纸片使AB边与对角线AC重合，点B落在点F处，折痕为AE，且EF=3．则AB的长为（ ）

A．3

B．4

C．5

D．6

如图，菱形OABC的顶点B在y轴上，顶点C的坐标为（﹣2，1），若反比例函数（x＞0）的图象经过点A，则k的值为（ ）

A．2

B．1

C．﹣1

D．﹣2

点A、B、C是平面内不在同一条直线上的三点，点D是平面内任意一点，若A、B、C、D四点恰能构成一个平行四边形，则在平面内符合这样条件的点D有（ ）
A.1个 B.2个 C.3个 D.4个

若△ABC的周长是12cm，则△ABC三条中位线围成的三角形的周长为（ ）

A．24cm

B．6cm

C．4cm

D．3cm

矩形、菱形、正方形都具有的性质是（ ）

A．对角线相等	B．对角线互相平分
C．对角线互相垂直	D．对角线平分对角

过多边形某个顶点的所有对角线，将这个多边形分成7个三角形，这个多边形是（   ）

A．八边形

B．九边形

C．十边形

D．十一边形