D、E分别是△ABC的边AB、AC的中点.O是平面上的一动点,连接OB、OC,G、F分别是OB、OC的中点,顺次连接点D、E、F、G.
(1)如图1,当点O在△ABC内时,求证:四边形DEFG是平行四边形;
(2)若点O在△ABC外,其余条件不变,点O的位置应满足什么条件,能使四边形DEFG是菱形?请在画2中补全图形,并说明理由.
如图,四边形 内接于 , ,点 在 的延长线上,且 .
(1)求证: 是 的切线;
(2)若 ,当 , 时,求 的长.

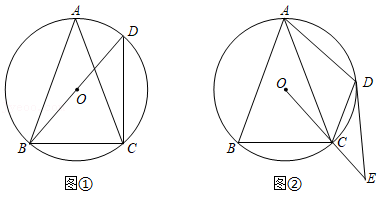
已知 内接于 , , ,点 是 上一点.
(Ⅰ)如图①,若 为 的直径,连接 ,求 和 的大小;
(Ⅱ)如图②,若 ,连接 ,过点作 的切线,与 的延长线交于点 ,求 的大小.
如图,四边形 内接于 , ,延长 到点 ,使得 ,连接 .
(1)求证: ;
(2)若 , , ,求 的值.

如图,在以线段 为直径的 上取一点 ,连接 、 .将 沿 翻折后得到 .
(1)试说明点 在 上;
(2)在线段 的延长线上取一点 ,使 .求证: 为 的切线;
(3)在(2)的条件下,分别延长线段 、 相交于点 ,若 , ,求线段 的长.

如图,在 中, ,以 为直径的 与边 , 分别交于 , 两点,过点 作 于点 .
(1)判断 与 的位置关系,并说明理由;
(2)求证: 为 的中点;
(3)若 , ,求 的长.

如图,在中,
,
是
上一点,
经过点
、
、
,交
于点
,过点
作
,交
于点
.
求证:(1)四边形是平行四边形;
(2).

如图,在菱形 中,对角线
中,对角线 与
与 相交于点
相交于点 ,
, ,在菱形
,在菱形 的外部以
的外部以 为边作等边三角形
为边作等边三角形 。点
。点 是对角线
是对角线 上一动点(点
上一动点(点 不与点
不与点 、D重合),将线段
、D重合),将线段 绕点
绕点 顺时针方向旋转
顺时针方向旋转 得到线段
得到线段 ,连接
,连接 。
。
(1)求 的长;
的长;
(2)如图2,当点 在线段
在线段 上,且点
上,且点 三点在同一条直线上时,求证:
三点在同一条直线上时,求证:
(3)连接 ,若
,若 的面积为40,请画出图形,并直接写出
的面积为40,请画出图形,并直接写出 的周长。
的周长。
如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
如图,点P是正方形ABCD内一点,点P到点A,B和D的距离分别为1, ,
, .△ADP沿点A旋转至△ABP’,连结PP’,并延长AP与BC相交于点Q.
.△ADP沿点A旋转至△ABP’,连结PP’,并延长AP与BC相交于点Q.
(1)求证:△APP’是等腰直角三角形;
(2)求∠BPQ的大小;
(3)求CQ的长.
小华参加学校的社团活动,需要摆放一个平行四边形的木框做道具,他手里有七根木条,长度分别为①40cm②50cm③40cm④60cm⑤50cm⑥90cm⑦100cm,若木条不能折断,请你帮他选一选,用几条可以摆成一个平行四边形?写出一种方案,并说明理由.
试题篮
()