如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴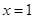 交z轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
交z轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.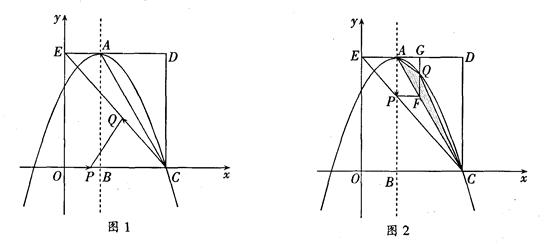
(1)填空:点A坐标为 ,抛物线的解析式为 ;
(2)在图1中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.连接PQ,是否存在实数t,使得PQ所在的直线经过点D,若存在,求出t的值;若不存在,请说明理由;
(3)在图2中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
如图,已知正比例函数 和反比例函数的图象交于点A(m,-2).
和反比例函数的图象交于点A(m,-2).
(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移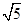 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
已知在矩形 中,
中, 是边
是边 上的一动点,联结
上的一动点,联结 、
、 ,过点
,过点 作射线交线段
作射线交线段 的延长线于点
的延长线于点 ,交边
,交边 于点
于点 ,且使得
,且使得 ,如果
,如果 ,
, ,
, ,
, ;
;
(1)求 关于
关于 的函数解析式,并写出它的定义域;
的函数解析式,并写出它的定义域;
(2)当 时,求
时,求 的正切值;
的正切值;
(3)如果△ 是以
是以 为底角的等腰三角形,求
为底角的等腰三角形,求 的长;
的长;
已知:如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=6,AB=3.E为BC边上一点,以BE为边作正方形BEFG,使正方形BEFG和梯形ABCD在BC的同侧.
(1)当正方形的顶点F恰好落在对角线AC上时,求BE的长;
(2)将(1)问中的正方形BEFG沿BC向右平移,记平移中的正方形BEFC为正方形B′EFG,当点E与点C重合时停止平移.设平移的距离为t,正方形B′EFG的边EF与AC交于点M,连接B′D,B′M,DM,是否存在这样的t,使△B′DM是直角三角形?若存在,求出t的值;若不存在,请说明理由.
如图,折叠矩形ABCD的一边AD使点D落在BC边上的E处,已知折痕AF=10cm,且tan∠FEC= .
.
(1)求矩形ABCD的面积;
(2)利用尺规作图求作与四边形AEFD各边都相切的⊙O的圆心O(只须保留作图痕迹),并求出⊙O的半径.
一块直角三角形木板的一条直角边 AB 的长为1.5米,面积为1.5米 2 ,要把它加工成一个面积最大的正方形桌面,甲、乙两位同学的加工方法分别如图所示,请你用所学的知识说明哪位同学的加工方法符合要求(加工损耗忽略不计,计算结果中的分数可保留).
如图,在△ABD中,AB=AD,AO平分∠BAD,过点D作AB的平行线交AO的延长线于点C,连接BC
(1)求证:四边形ABCD是菱形。
(2)如果OA,OB(OA>OB)的长(单位:米)是一元二次方程 的两根,求AB的长以及菱形ABCD的面积。
的两根,求AB的长以及菱形ABCD的面积。
(3)若动点M从A出发,沿AC以2m/S的速度匀速直线运动到点C,动点N从B 出发,沿BD以1m/S的速度匀速直线运动到点D,当M运动到C点时运动停止。若M、N同时出发,问出发几秒钟后,△MON的面积为 ?
?
如图,正方形ABCD的边长为1,点E是AD边上的动点,从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,连接CG.请探究:
(1)线段AE与CG是否相等?请说明理由.
(2)若设 ,
, ,当
,当 取何值时,
取何值时, 最大?
最大?
(3)连接BH,当点E运动到AD的何位置时,△BEH∽△BAE?
已知两个连体的正方形(有两条边在同一条直线上)在正方形网格上的位置如图所示,请你把它分割后,拼接成一个新的正方形. (要求:在正方形网格图中用实线画出拼接成的新正方形且新正方形的顶点在网格的格点上,不写作法).
如图,四边形ABCD、DEFG都是正方形,连接AE、CG,AE与CG相交于点M,CG与AD相交于点N。求证:

如图所示,已知正方形ABCD,直角三角形纸板的一个锐角顶点与点A重合,纸板绕点A旋转时,直角三角形纸板的一边与直线CD交于E,分别过B、D作直线AE的垂线,垂足分别为F、G.
(1)当点E在DC延长线上时,如图①,求证:BF = DG一FG;
(2)将图①中的三角板绕点A逆时针旋转得图②、图③,此时BF、FG、DG之间又有怎样的数量关系?请直接写出结论(不必证明).
如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连接EF与边CD相交于点G,连接BE与对角线AC相交于点H, AE=CF,BE=EG。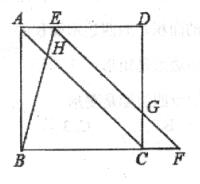
(1)求证:EF//AC;
(2)求∠BEF大小;
(3)求证: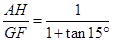
如图1,小明将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得AB=5,AD=4.在进行如下操作时遇到了下面的几个问题,请你帮助解决.

(1)将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时,EF恰好经过点A(如图2),请你求出AE和FG的长度.
(2)在(1)的条件下,小明先将三角形的边EG和矩形边AB重合,然后将△EFG沿直线BC向右平移,至F点与B重合时停止.在平移过程中,设G点平移的距离为x,两纸片重叠部分面积为y,求在平移的整个过程中,y与x的函数关系式,并求当重叠部分面积为10时,平移距离x的值(如图3).
(3)在(2)的操作中,小明发现在平移过程中,虽然有时平移的距离不等,但两纸片重叠的面积却是相等的;而有时候平移的距离不等,两纸片重叠部分的面积也不可能相等.请探索这两种情况下重叠部分面积y的范围(直接写出结果).
如图,正方形ABCD的边AD与矩形EFGH的边FG重合,将正方形ABCD以1cm/s的速度沿FG方向移动,移动开始前点A与点F重合,在移动过程中,边AD始终与边FG重合,连接CG,过点A作CG的平行线交线段GH于点P,连接PD.已知正方形ABCD的边长为1cm,矩形EFGH的边FG,GH的长分别为4cm,3cm,设正方形移动时间为x(s),线段GP的长为y(cm),其中0≤x≤2.5.
(1)试求出y关于x的函数关系式,并求当y=3时相应x的值;
(2)记△DGP的面积为S1,△CDG的面积为S2.试说明S1-S2是常数;
(3)当线段PD所在直线与正方形ABCD的对角线AC垂直时,求线段PD的长.
试题篮
()