初中数学圆内接四边形的性质解答题

我们知道平行四边形有很多性质.
现在如果我们把平行四边形沿着它的一条对角线翻折，会发现这其中还有更多的结论.
【发现与证明】ABCD中，AB≠BC，将△ABC沿AC翻折至△AB′C，连结B′D.
结论1：B′D∥AC；
结论2：△AB′C与ABCD重叠部分的图形是等腰三角形.
……
请利用图1证明结论1或结论2（只需证明一个结论）.
【应用与探究】在ABCD中，已知∠B=30°，将△ABC沿AC翻折至△AB′C，连结B′D.
（1）如图1，若，则∠ACB=       °，BC=       ；
（2）如图2，，BC=1，AB′与边CD相交于点E，求△AEC的面积；
（3）已知，当BC长为多少时，是△AB′D直角三角形？

如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．
（1）求证：CE=CF；
（2）在图1中，若G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？
（3）根据你所学的知识，运用（1）、（2）解答中积累的经验，完成下列各题：
①如图2，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B=90°，AB=BC=12，E是AB的中点，且∠DCE=45°，求DE的长；
②如图3，在△ABC中，∠BAC=45°，AD⊥BC，BD=2，CD=3，则△ABC的面积为　_________　（直接写出结果，不需要写出计算过程）．

如图，两个边长均为2的正方形ABCD和正方形CDEF，点B、C、F在同一直线上，一直角三角板的直角顶点放置在D点处，DP交AB于点M，DQ交BF于点N．
（1）求证：△DBM≌△DFN；
（2）延长正方形的边CB和EF，分别与直角三角板的两边DP、DQ（或它们的延长线）交于点G和点H，试探究下列问题：
①线段BG与FH相等吗？说明理由；
②当线段FN的长是方程的一根时，试求出的值．

如图所示，在菱形ABCD中，AB=4，∠BAD=120°，△AEF为正三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．
（1）证明不论E、F在BC、CD上如何滑动，总有BE=CF；
（2）当点E、F在BC、CD上滑动时，分别探讨四边形AECF和△CEF的面积是否发生变化？如果不变，求出这个定值；如果变化，求出最大（或最小）值．

如图，在正方形ABCD中，点E、F分别是BC、CD的中点，DE交AF于点M，点N为DE的中点．
（1）若AB=4，求△DNF的周长及sin∠DAF的值；
（2）求证：2AD•NF=DE•DM．

在正方形ABCD 中，点F是BC延长线上一点，过点B作BE⊥DF于点E，交CD于点G，连接CE.
（1）若正方形ABCD边长为3，DF=4，求CG的长；
（2）求证：EF+EG=CE.

（1）图①是将线段AB向右平移1个单位长度，图②是将线段AB折一下再向右平移1个单位长度，请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形﹒
（2）若长方形的长为a，宽为b，请分别写出三个图形中除去阴影部分后剩余部分的面积﹒
（3）如图④，在宽为10m，长为40m的长方形菜地上有一条弯曲的小路，小路宽为1m，求这块菜地的面积﹒

如图，在线段AE的同侧作正方形ABCD和正方形BEFG（BE＜AB），连接EG并延长交DC于点M，作MN⊥AB，垂足为N，MN交BD于点P，设正方形ABCD的边长为1．
（1）证明：四边形MPBG是平行四边形；
（2）设BE=x，四边形MNBG的面积为y，求y关于x的函数关系式，并写出自变量x的取值范围；
（3）如果按题设作出的四边形BGMP是菱形，求BE的长．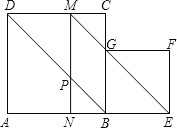

如图，在Rt△ABC中，∠BAC=90°，∠B=60°，BC=16cm，AD是斜边BC上的高，垂足为D，BE=1cm．点M从点B出发沿BC方向以1cm/s的速度运动，点N从点E出发，与点M同时同方向以相同的速度运动，以MN为边在BC的上方作正方形MNGH．点M到达点D时停止运动，点N到达点C时停止运动．设运动时间为t（s）．
（1）当t为何值时，点G刚好落在线段AD上？
（2）设正方形MNGH与Rt△ABC重叠部分的图形的面积为S，当重叠部分的图形是正方形时，求出S关于t的函数关系式并写出自变量t的取值范围．
（3）设正方形MNGH的边NG所在直线与线段AC交于点P，连接DP，当t为何值时，△CPD是等腰三角形？

如图，等腰梯形ABCD中，AD∥BC，AD=AB=CD=2，∠C=60°，M是BC的中点．
（1）求证：△MDC是等边三角形；
（2）将△MDC绕点M旋转，当MD（即MD′）与AB交于一点E，MC（即MC′）同时与AD交于一点F时，点E，F和点A构成△AEF．试探究△AEF的周长是否存在最小值？如果不存在，请说明理由；如果存在，请计算出△AEF周长的最小值．
 

如图①，已知等腰梯形ABCD的周长为48，面积为S，AB∥CD，∠ADC=60°，设AB=3x．
（1）用x表示AD和CD；
（2）用x表示S，并求S的最大值；
（3）如图②，当S取最大值时，等腰梯形ABCD的四个顶点都在⊙O上，点E和点F分别是AB和CD的中点，求⊙O的半径R的值．

如图，已知∠MON=90°，A是∠MON内部的一点，过点A作AB⊥ON，垂足为点B，AB=3厘米，OB=4厘米，动点E，F同时从O点出发，点E以1.5厘米/秒的速度沿ON方向运动，点F以2厘米/秒的速度沿OM方向运动，EF与OA交于点C，连接AE，当点E到达点B时，点F随之停止运动．设运动时间为t秒（t＞0）．
（1）当t=1秒时，△EOF与△ABO是否相似？请说明理由；
（2）在运动过程中，不论t取何值时，总有EF⊥OA．为什么？
（3）连接AF，在运动过程中，是否存在某一时刻t，使得S_△AEF=S_{四边形ABOF}？若存在，请求出此时t的值；若不存在，请说明理由．

如图1，边长为4的正方形ABCD中，点E在AB边上（不与点A，B重合），点F在BC边上（不与点B，C重合）．
第一次操作：将线段EF绕点F顺时针旋转，当点E落在正方形上时，记为点G；
第二次操作：将线段FG绕点G顺时针旋转，当点F落在正方形上时，记为点H；
依次操作下去…
（1）图2中的△EFD是经过两次操作后得到的，其形状为　 　，求此时线段EF的长；
（2）若经过三次操作可得到四边形EFGH．
①请判断四边形EFGH的形状为　 　，此时AE与BF的数量关系是　 　；
②以①中的结论为前提，设AE的长为x，四边形EFGH的面积为y，求y与x的函数关系式及面积y的取值范围；
（3）若经过多次操作可得到首尾顺次相接的多边形，其最大边数是多少？它可能是正多边形吗？如果是，请直接写出其边长；如果不是，请说明理由．

在矩形ABCD中，，点G，H分别在边AB，DC上，且HA=HG，点E为AB边上的一个动点，连接HE，把△AHE沿直线HE翻折得到△FHE．
（1）如图1，当DH=DA时，
①填空：∠HGA=       度；
②若EF∥HG，求∠AHE的度数，并求此时a的最小值；
（2）如图3，∠AEH=60°，EG=2BG，连接FG，交边FG，交边DC于点P，且FG⊥AB，G为垂足，求a的值．

在菱形ABCD和正三角形BGF中，∠ABC=60°，P是DF的中点，连接PG、PC．
（1）如图1，当点G在BC边上时，易证：PG=PC．（不必证明）
（2）如图2，当点F在AB的延长线上时，线段PC、PG有怎样的数量关系，写出你的猜想，并给与证明；
（3）如图3，当点F在CB的延长线上时，线段PC、PG又有怎样的数量关系，写出你的猜想（不必证明）．