初中数学圆内接四边形的性质填空题

如图，正方形ABCD中，点E、F分别在AB、BC上，DH⊥EF于H，DA=HD，EH=2，HF=3．则正方形ABCD的边长为         ．

有一张一个角为30°，最小边长为4的直角三角形纸片，沿图中所示的中位线剪开后，将两部分拼成一个四边形，所得四边形的周长是             ．

如图，矩形ABCD的对角线AC=10，BC=8，则图中五个小矩形的周长之和为_______．

如图，设四边形ABCD是边长为1的正方形，以对角线AC为边作第二个正方形ACEF、再以对角线AE为边作笫三个正方形AEGH，如此下去…．若正方形ABCD的边长记为a₁，按上述方法所作的正方形的边长依次为a₂，a₃，a₄，…，a_n，则a_n=          ．

将两块全等的含30°角的三角尺如图1摆放在一起，设较短直角边为1，如图2，将Rt△BCD沿射线BD方向平移，在平移的过程中，当点B的移动距离为        时，四边ABC₁D₁为矩形；当点B的移动距离为          时，四边形ABC₁D₁为菱形．

如图，正六边形硬纸片ABCDEF在桌面上由图1的起始位置沿直线l不滑行地翻滚一周后到图2位置．若正六边形的边长为2cm，则正六边形的中心O运动的路程为         cm．

如图，在菱形ABCD中，AB=6，∠ABC=60°，点E在AD上，且AE=2，点P是对角线BD上的一个动点，则PE+PA的最小值是                    ．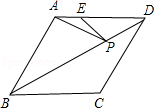

已知正方形ABC₁D₁的边长为1，延长C₁D₁到A₁，以A₁C₁为边向右作正方形A₁C₁C₂D₂，延长C₂D₂到A₂，以A₂C₂为边向右作正方形A₂C₂C₃D₃（如图所示），以此类推…，若A₁C₁=2，且点A，D₂， D₃，…，D₁₀都在同一直线上，则正方形A₉C₉C₁₀D₁₀的边长是__________________________

如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连结BD、DP，BD与CF相交于点H．给出下列结论：
①△ABE≌△DCF；②；③；④．
其中正确的是         ．（写出所有正确结论的序号）

如图，已知菱形ABCD的对角线AC=2，∠BAD=60°，BD边上有2013个不同的点p₁，p₂，…，p₂₀₁₃，过p_i（i=1，2，…，2013）作P_iE_i⊥AB于E_i，P_iF_i⊥AD于F_i，则P₁E₁+P₁F₁+P₂E₂+P₂F₂+…P₂₀₁₃E₂₀₁₃+P₂₀₁₃F₂₀₁₃的值为            ．

如图，菱形纸片ABCD中，∠A=60°，将纸片折叠，点A、D分别落在A′、D′处，且A′D′经过B，EF为折痕，当D′F⊥CD时，的值为    ．

对正方形ABCD进行分割，如图1，其中E、F分别是BC、CD的中点，M、N、G分别是OB、OD、EF的中点，沿分化线可以剪出一副“七巧板”，用这些部件可以拼出很多图案，图2就是用其中6块拼出的“飞机”．若△GOM的面积为1，则“飞机”的面积为     ．

如图1，在正方形ABCD中，延长BC至M，使BM=DN，连接MN交BD延长线于点E．

（1）求证：BD+2DE=BM ．
（2）如图2，连接BN交AD于点F，连接MF交BD于点G．若AF:FD=1:2，且CM=2，则线段DG=_______．

已知菱形ABCD边长为5cm，tan∠DAB=,连接AC、BD,过点B作BE⊥AB分别交AC、CD于E、F。若点P为AD上一点，且∠DPE+∠DAB=90⁰,则AP长为          ．

如图，菱形OABC的面积为3，顶点O的坐标为（0，0），顶点A的坐标为（3，0），顶点B在第一象限，边BC与y轴交于点D，点E在边OA上．将四边形ABDE沿直线DE翻折，使点A落在第四象限的点F处，且FE⊥EA．则直线OF的解析式为        。