如图, 为 的直径, 切 于点 ,与 的延长线交于点 , 交 于点 ,连接 、 、 ,过点 作 于点 ,延长 交 于点 .
(1)求证: ;
(2)连接 ,若 , ,求线段 的长.

如图,在 中,以 为直径的 分别与 , 相交于点 , , ,过点 作 的切线交边 于点 .
(1)求证: ;
(2)若 的半径为5, ,求 的长(结果保留 .

如图, 是 的直径,点 在 的延长线上, 与 相切于点 , ,交 的延长线于点 .
(1)求证: ;
(2)若 , ,求 的长.

如图, 中, , 为 的平分线,以 上一点 为圆心的半圆经过 、 两点,交 于 ,连接 交 于点 .
(1)判断 与 的位置关系,并说明理由;
(2)若 , ,求 的长.

如图,在等腰 中, ,以 为直径的 与 相交于点 ,过点 作 交 延长线于点 ,垂足为点 .
(1)判断 与 的位置关系,并说明理由;
(2)若 的半径 , ,求 的长.

如图, 中, ,以 为直径的 交 于点 , 、 是 上两点,连接 、 、 ,满足 .
(1)求证: 是 的切线;
(2)若 的半径为3, ,求 的长.

如图,在 中, , 于点 , 是 上一点,以 为直径的 交 于点 ,连接 ,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.

如图, 是 直径,点 在 上, 平分 , 是 的切线, 与 相交于点 .
(1)求证: ;
(2)若 , ,求 的长.

如图,以 的边 为直径的 交 边于点 ,交 边于点 ,连接 ,过点 的切线交 的延长线于点 , .
(1)求证: 为等腰三角形.
(2)求证: .

如图, 内接于 , 的边 是 的直径,且 ,连接 .
(1)求证: 是 的切线.
(2)若 , ,求 与弦 围成的阴影部分的面积.

如图,在平行四边形 中, ,垂足为点 ,以 为直径的 与边 相切于点 ,连接 交 于点 ,连接 .
(1)求证: .
(2)若 ,求 的值.
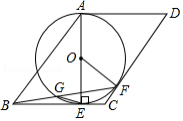
如图,在 中, ,以点 为圆心、 的长为半径的 恰好经过 的中点 ,连接 , , , 与 交于点 .
(1)求证: 与 相切.
(2)若 ,求 的长.

如果三角形三边的长 、 、 满足 ,那么我们就把这样的三角形叫做“匀称三角形”,如:三边长分别为1,1,1或3,5,7, 的三角形都是“匀称三角形”.
(1)如图1,已知两条线段的长分别为 、 .用直尺和圆规作一个最短边、最长边的长分别为 、 的“匀称三角形”(不写作法,保留作图痕迹);
(2)如图2, 中, ,以 为直径的 交 于点 ,过点 作 的切线交 延长线于点 ,交 于点 ,若 ,判断 是否为“匀称三角形”?请说明理由.

如图, 是 的直径, 是 的弦,直线 与 相切于点 ,过点 作 于点 .
(1)求证: ;
(2)若 , ,则 的半径是 .

试题篮
()