如图, 是 的直径,弦 ,垂足为 ,连接 ,过 上一点 作 交 的延长线于点 ,连接 交 于点 ,且 ,连接 .
(1)求证: ;
(2)求证: 是 的切线;
(3)延长 交 的延长线于点 ,若 , ,求 的值.

通过对下面数学模型的研究学习,解决问题.
【模型呈现】
如图,在 , ,将斜边 绕点 顺时针旋转 得到 ,过点 作 于点 ,可以推理得到 ,进而得到 , .
我们把这个数学模型称为“ 型”.
推理过程如下:

【模型应用】
如图,在 内接于 , , ,将斜边 绕点 顺时针旋转一定的角度得到 ,过点 作 于点 , , ,连接 交 于点 .

(1)求证: 是 的切线;
(2)连接 交 于点 ,连接 .求证: .
如图, 为 的直径, 为 上一点, 为 延长线上一点, .
(1)求证: 为 的切线;
(2)线段 分别交 , 于点 , 且 , 的半径为5, ,求 的长.
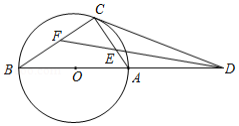
如图,在 中, 为直角, , ,半径为2的动圆圆心 从点 出发,沿着 方向以1个单位长度 秒的速度匀速运动,同时动点 从点 出发,沿着 方向也以1个单位长度 秒的速度匀速运动,设运动时间为 秒 以 为圆心, 长为半径的 与 、 的另一个交点分别为 、 ,连接 、 .
(1)当 为何值时,点 与点 重合?
(2)当 经过点 时,求 被 截得的弦长.
(3)若 与线段 只有一个公共点,求 的取值范围.
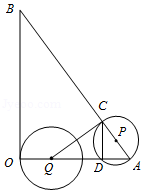
如图,在 中, , 的平分线交 于点 , ,以点 为圆心 为半径作半圆.
(1)求证: 为 的切线;
(2)如果 ,求 的值.

如图, 为 直径, 为 上一点,点 是 的中点, 于 , 于 .
(1)判断 与 的位置关系,并证明你的结论;
(2)若 ,求 的长度.

如图, 内接于 , 为 的直径, 与 相交于点 , 的延长线与过点 的直线相交于点 ,且 .
(1)求证: 是 的切线;
(2)已知 ,且 与 、 分别相交于点 、 ,若 , , ,求 的值.

如图,在 中, ,以 边为直径作 交 边于点 ,过点 作 于点 , 、 的延长线交于点 .
(1)求证: 是 的切线;
(2)若 ,且 ,求 的半径与线段 的长.

如图,以 的 边上一点 为圆心,经过 , 两点且与 边交于点 ,点 为 的下半圆弧的中点,连接 交线段 于点 ,若 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径 及 .

如图,在平面直角坐标系 中,以点 为圆心的圆分别交 轴的正半轴于点 ,交 轴的正半轴于点 .劣弧 的长为 ,直线 与 轴、 轴分别交于点 、 .
(1)求证:直线 与 相切;
(2)求图中所示的阴影部分的面积(结果用 表示)

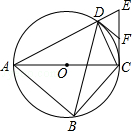
如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
(1)求 的度数;
(2)求证:DF是⊙O的切线;
(3)若 ,求 的值.
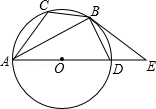
如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且 .
(1)求证:直线MN是⊙O的切线;
(2)若 , ,求⊙O的半径.

如图,△ABC是⊙O的内接三角形,AB为直径,过点B的切线与AC的延长线交于点D,E是BD中点,连接CE.
(1)求证:CE是⊙O的切线;
(2)若AC=4,BC=2,求BD和CE的长.

如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且 ,延长AD到E,且有 .
(1)求证:BE是⊙O的切线;
(2)若 , ,求圆的直径AD及切线BE的长.
试题篮
()