我们在学完“平移、轴对称、旋转”三种图形的变化后,可以进行进一步研究,请根据示例图形,完成下表.
图形的变化 |
示例图形 |
与对应线段有关的结论 |
与对应点有关的结论 |
平移 |
|
(1) |
|
轴对称 |
|
(2) |
(3) |
旋转 |
|
;对应线段 和 所在的直线相交所成的角与旋转角相等或互补. |
(4) |
如图1,该几何体是由5个棱长为1个单位长度的正方体摆放而成,将正方体 向右平移2个单位长度后(如图 ,所得几何体的视图

A.主视图改变,俯视图改变B.主视图不变,俯视图不变
C.主视图改变,俯视图不变D.主视图不变,俯视图改变
已知点 的坐标为 ,点 的坐标为 .将线段 沿某一方向平移后,点 的对应点的坐标为 .则点 的对应点的坐标为
A. B. C. D.
如图, 为坐标原点, 是等腰直角三角形, ,点 的坐标为 , ,将该三角形沿 轴向右平移得到 △ ,此时点 的坐标为 , ,则线段 在平移过程中扫过部分的图形面积为 .

如图,把 放在直角坐标系内,其中 , ,点 、 的坐标分别为 、 ,将 沿 轴向右平移,当点 落在直线 上时,线段 扫过的面积为 .

如图, 沿着 方向平移得到△ ,点 是直线 上任意一点,若 ,△ 的面积分别为 , ,则下列关系正确的是
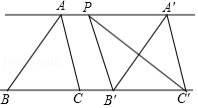
A. B. C. D.
如图,面积为6的平行四边形纸片 中, , ,按下列步骤进行裁剪和拼图.

第一步:如图①,将平行四边形纸片沿对角线 剪开,得到 和 纸片,再将 纸片沿 剪开 为 上任意一点),得到 和 纸片;
第二步:如图②,将 纸片平移至 处,将 纸片平移至 处;
第三步:如图③,将 纸片翻转过来使其背面朝上置于 处(边 与 重合, 和 在 同侧),将 纸片翻转过来使其背面朝上置于 处,(边 与 重合, 和 在 同侧).
则由纸片拼成的五边形 中,对角线 长度的最小值为 .
如图,已知 A(6,0), B(8,5),将线段 OA平移至 CB,点 D在 x轴正半轴上(不与点 A重合),连接 OC, AB, CD, BD.
(1)求对角线 AC的长;
(2)设点 D的坐标为( x,0),△ ODC与△ ABD的面积分别记为 S 1, S 2.设 S= S 1﹣ S 2,写出 S关于 x的函数解析式,并探究是否存在点 D使 S与△ DBC的面积相等?如果存在,用坐标形式写出点 D的位置;如果不存在,说明理由.

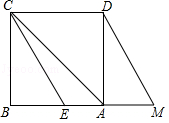
如图,已知正方形 ABCD,点 M是边 BA延长线上的动点(不与点 A重合),且 AM< AB,△ CBE由△ DAM平移得到.若过点 E作 EH⊥ AC, H为垂足,则有以下结论:①点 M位置变化,使得∠ DHC=60°时,2 BE= DM;②无论点 M运动到何处,都有 DM= HM;③无论点 M运动到何处,∠ CHM一定大于135°.其中正确结论的序号为 .
如图,在平面直角坐标系中,直线y=2x与反比例函数 在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数 在第一象限内的图象交于点P,且△POA的面积为2.
(1)求k的值.
(2)求平移后的直线的函数解析式.

已知反比例函数 .
(1)若该反比例函数的图象与直线 只有一个公共点,求k的值;
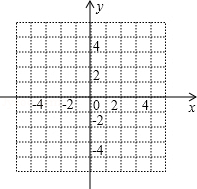
(2)如图,反比例函数 的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移至C2处所扫过的面积.
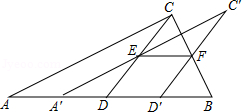
如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.
如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ACED为菱形的是( )

A.AB=BCB.AC=BCC.∠B=60°D.∠ACB=60°
如图,△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm.将线段DC沿着CB的方向平移7cm得到线段EF,点E,F分别落在边AB,BC上,则△EBF的周长为 cm.

试题篮
()