如图,在矩形中,
,
,点
为
边上一个动点,连接
,将线段
绕点
顺时针旋转
,点
落在点
处,当点
在矩形
外部时,连接
、
.若
为直角三角形,则
的长 .

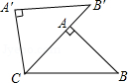
如图,在 中, ,将 绕点 按逆时针方向旋转 得到 △ ,点 在边 上,则 的大小为
| A. |
|
B. |
|
C. |
|
D. |
|
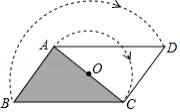
如图,将
绕边
的中点
顺时针旋转
.嘉淇发现,旋转后的
与
构成平行四边形,并推理如下: 
小明为保证嘉淇的推理更严谨,想在方框中" ,"和" 四边形 "之间作补充,下列正确的是
| A. |
嘉淇推理严谨,不必补充 |
B. |
应补充:且 |
| C. |
应补充:且 |
D. |
应补充:且 |
对于题目:"如图1,平面上,正方形内有一长为12、宽为6的矩形,它可以在正方形的内部及边界通过移转(即平移或旋转)的方式,自由地从横放移转到竖放,求正方形边长的最小整数 ."甲、乙、丙作了自认为边长最小的正方形,先求出该边长 ,再取最小整数 .
甲:如图2,思路是当 为矩形对角线长时就可移转过去;结果取 .
乙:如图3,思路是当 为矩形外接圆直径长时就可移转过去;结果取 .
丙:如图4,思路是当 为矩形的长与宽之和的 倍时就可移转过去;结果取 .
下列正确的是

| A. |
甲的思路错,他的 值对 |
| B. |
乙的思路和他的 值都对 |
| C. |
甲和丙的 值都对 |
| D. |
甲、乙的思路都错,而丙的思路对 |
已知正方形 和正六边形 边长均为1,把正方形放在正六边形中,使 边与 边重合,如图所示,按下列步骤操作:
将正方形在正六边形中绕点 顺时针旋转,使 边与 边重合,完成第一次旋转;再绕点 顺时针旋转,使 边与 边重合,完成第二次旋转; 在这样连续6次旋转的过程中,点 , 间的距离可能是

| A. |
1.4 |
B. |
1.1 |
C. |
0.8 |
D. |
0.5 |
已知,
为射线
上一定点,
,
为射线
上一点,
为线段
上一动点,连接
,满足
为钝角,以点
为中心,将线段
顺时针旋转
,得到线段
,连接
.
(1)依题意补全图1;
(2)求证:;
(3)点关于点
的对称点为
,连接
.写出一个
的值,使得对于任意的点
总有
,并证明.
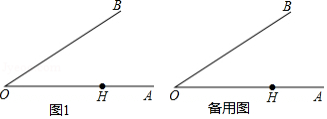
(1)如图,把∠AOB绕着O点按逆时针方向旋转一个角度,得∠A′OB′,指出图中所有相等的角.
(2)如图,BD平分∠ABC,BE分∠ABC分2:5两部分,∠DBE=21°,求∠ABC的度数.
如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=﹣ 、y=
、y= 的图象交于B、A两点,则∠OAB的大小的变化趋势为( )
的图象交于B、A两点,则∠OAB的大小的变化趋势为( )

A.逐渐变小 B.逐渐变大 C.无法确定 D.保持不变
如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
试题篮
()