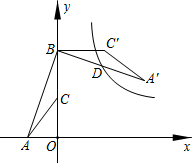
如图,点 的坐标是 ,点 的坐标是 , 为 的中点,将 绕点 逆时针旋转 后得到△ .若反比例函数 的图象恰好经过 的中点 ,则 的值是
| A. |
9 |
B. |
12 |
C. |
15 |
D. |
18 |
小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.

(一猜测探究
在中,
,
是平面内任意一点,将线段
绕点
按顺时针方向旋转与
相等的角度,得到线段
,连接
.
(1)如图1,若是线段
上的任意一点,请直接写出
与
的数量关系是
,
与
的数量关系是 ;
(2)如图2,点是
延长线上点,若
是
内部射线
上任意一点,连接
,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由.
(二拓展应用
如图3,在△中,
,
,
,
是
上的任意点,连接
,将
绕点
按顺时针方向旋转
,得到线段
,连接
.求线段
长度的最小值.
如图,和
是有公共顶点的等腰直角三角形,
.

(1)如图1,连接,
,
的延长线交
于点
,交
于点
,求证:
;
(2)如图2,把绕点
顺时针旋转,当点
落在
上时,连接
,
,
的延长线交
于点
,若
,
,求
的面积.
如图1,在中,
,
,
,点
、
分别是边
、
的中点,连接
.将
绕点
逆时针方向旋转,记旋转角为
.
(1)问题发现
①当时,
;
②当时,
.
(2)拓展探究
试判断:当时,
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
绕点
逆时针旋转至
、
、
三点在同一条直线上时,求线段
的长.

(1)如图1,是正方形
边
上的一点,连接
、
,将
绕点
逆时针旋转
,旋转后角的两边分别与射线
交于点
和点
.
①线段和
的数量关系是 ;
②写出线段,
和
之间的数量关系.
(2)当四边形为菱形,
,点
是菱形
边
所在直线上的一点,连接
、
,将
绕点
逆时针旋转
,旋转后角的两边分别与射线
交于点
和点
.
①如图2,点在线段
上时,请探究线段
、
和
之间的数量关系,写出结论并给出证明;
②如图3,点在线段
的延长线上时,
交射线
于点
,若
,
,直接写出线段
的长度.

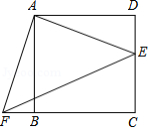
如图,四边形 是边长为5的正方形, 是 上一点, ,将 绕着点 顺时针旋转到与 重合,则
| A. |
|
B. |
|
C. |
|
D. |
|
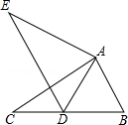
如图,在 中, , , ,将 绕点 顺时针旋转得到 ,当点 的对应点 恰好落在 边上时,则 的长为
| A. |
1.6 |
B. |
1.8 |
C. |
2 |
D. |
2.6 |
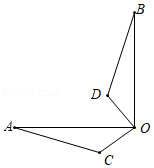
如图,在 中, , ,将 绕点 顺时针旋转 后得到 ,则 边在旋转过程中所扫过的图形的面积为 .
| A. |
|
B. |
|
C. |
|
D. |
|
如图,直线与
轴,
轴分别交于
,
两点,过
,
两点的抛物线
与
轴交于点
.
(1)求抛物线的解析式;
(2)连接,若点
是线段
上的一个动点(不与
,
重合),过点
作
,交
于点
,当
的面积是
时,求点
的坐标;
(3)在(2)的结论下,将绕点
旋转
得△
,试判断点
是否在抛物线上,并说明理由.

试题篮
()