初中数学平行线分线段成比例试题

点A（x₁，y₁），B（x₂，y₂），C（x₃，y₃）都是反比例函数的图象上，若x₁＜x₂＜0＜x₃，则y₁，y₂，y₃的大小关系是（　　）

A．y3＜y1＜y2	B．y1＜y2＜y3
C．y3＜y2＜y1	D．y2＜y1＜y3

点（﹣1，y₁），（2，y₂），（3，y₃）均在函数的图象上，则y₁，y₂，y₃的大小关系是（　　）

A．y3＜y2＜y1	B．y2＜y3＜y1
C．y1＜y2＜y3	D．y1＜y3＜y2

如图所示，反比例函数图象上一点A，过A作AB⊥轴于B，若S_△AOB＝3，则反比例函数的解析式为

函数（为常数）的图象上有三点（－4，），（－1，），（2，），则函数值，，的大小关系是（   ）

A．＜＜	B．＜＜
C．＜＜	D．＜＜

如果双曲线过点（3，－2），那么下列的点在该双曲线上的是（   ）

A．（3，0）

B．（0，6）

C．（－1.25，8）

D．（－1.5，4）

下列函数的图像在每一个象限内，值随值的增大而增大的是（   ）

A．

B．

C．

D．

下列函数中，反比例函数是（　　　）

A．

B．

C．

D．

已知反比例函数y＝的图象上有A（x₁，y₁）、B（x₂，y₂）两点，当x₁＜x₂＜0时，y₁＜y₂，则m的取值范围是（　　）．

A．m＜0

B．m＞0

C．m＜

D．m＞

如图，正比例函数的图象与反比例函数在第一象限的图象交于点，过点作轴的垂线，垂足为，已知的面积为1.

（1）求反比例函数的解析式；
（2）如果为反比例函数在第一象限图象上的点（点与点不重合），且点的横坐标为1，在轴上求一点，使最小.

甲、乙两家商场进行促销活动，甲商场采用“满200减100”的促销方式，即购买商品的总金额满200元但不足400元，少付100元；满400元但不足600元，少付200元；……，乙商场按顾客购买商品的总金额打6折促销．
（1）若顾客在甲商场购买了510元的商品，付款时应付多少钱？
（2）若顾客在甲商场购买商品的总金额为x（400≤x＜600）元，优惠后得到商家的优惠率为p（p=），写出p与x之间的函数关系式，并说明p随x的变化情况；
（3）品牌、质量、规格等都相同的某种商品，在甲乙两商场的标价都是x（200≤x＜400）元，你认为选择哪家商场购买商品花钱较少？请说明理由．

若A(a₁，b₁)，B(a₂，b₂)是反比例函数y = –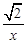图象上的两点，且a₁＜a₂，则b₁与b₂的大小关系是

A．b1＜b2

B．b1 = b2

C．b1＞b2

D．不能确定

已知点（x₁，－1），（x₂，2），（x₃，4），在函数ｙ＝(<0)的图象上，则x₁，x₂，x₃从小到大排列为              (用“＜”号连接）．

若反比例函数的图象在每一个象限中，y随着x的增大而减小，则m的取值范围是___________．

已知线段m、n、p、q的长度满足等式mn=pq，将它改写成比例式的形式，错误的是(     )

A．

B．

C．

D．

已知反比例函数的图象经过点P(一l，2)，则这个函数的图象位于（    ）

A．第二、三象限

B．第一、三象限

C．第三、四象限

D．第二、四象限