如图点P,Q是反比例函数 图象上的两点,PA⊥
图象上的两点,PA⊥ 轴于点A,QN⊥
轴于点A,QN⊥ 轴于点N,作PM⊥
轴于点N,作PM⊥ 轴于点M,QB⊥
轴于点M,QB⊥ 轴于点B,连结PB,QM,记△ABP的面积为S1,△QMN的面积为S2,则S1_____S2(填“>”或“<”或“=”)
轴于点B,连结PB,QM,记△ABP的面积为S1,△QMN的面积为S2,则S1_____S2(填“>”或“<”或“=”)
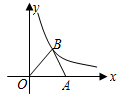
如图,在直角坐标系中,点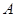 是
是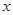 轴正半轴上的一个定点,点
轴正半轴上的一个定点,点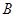 是双曲线
是双曲线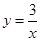 (
(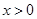 )上的一个动点,当点
)上的一个动点,当点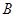 的横坐标逐渐增大时,
的横坐标逐渐增大时, 的面积将会( )
的面积将会( )
| A.逐渐增大 | B.不变 | C.逐渐减小 | D.先增大后减小 |
反比例函数 图象上有三个点
图象上有三个点 ,其中
,其中 ,则
,则 的大小关系是 ( )
的大小关系是 ( )
A.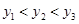 |
B. |
C.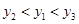 |
D. |
如图,已知正比例函数与反比例函数交于A(-1,2),B(1,-2)两点,当正比例函数的值大于反比例函数值时,x的取值范围为____________________.
如图,已知反比例函数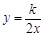 和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点。
和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点。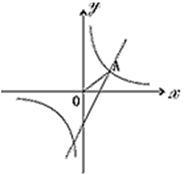
(1)求反比例函数的解析式;
(2)如图,已知点A在第一象限,且同时在上述两个函数的图象上, 求点A的坐标;
(3)利用(2)的结果,请问:在x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由。
如图,已知反比例函数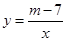 的图象的一支位于第一象限.
的图象的一支位于第一象限.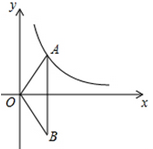
(1)求m的取值范围;
(2)O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.
如图,一次函数 的图像与反比例函数
的图像与反比例函数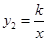 (
(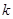 为常数,且
为常数,且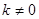 )的图像都经过点
)的图像都经过点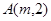
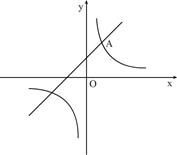
(1)求点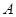 的坐标及反比例函数的表达式;
的坐标及反比例函数的表达式;
(2)结合图像直接比较:当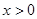 时,
时,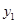 和
和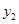 的大小.
的大小.
李明同时掷甲、乙两枚质地均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).记甲立方体朝上一面上的数字为x、乙立方体朝上一面朝上的数字为y,这样就确定点P的一个坐标( ,
, ),那么点P落在双曲线
),那么点P落在双曲线 上的概率为( )
上的概率为( )
A. |
B. |
C. |
D. |
如图是函数 与函数
与函数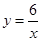 在第一象限内的图象,点
在第一象限内的图象,点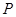 是
是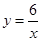 的图象上一动点,
的图象上一动点,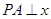 轴于点A,交
轴于点A,交 的图象于点
的图象于点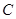 ,
,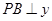 轴于点B,交
轴于点B,交 的图象于点
的图象于点 .
.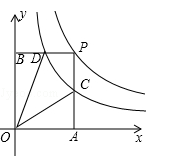
(1)求证:D是BP的中点;
(2)求出四边形ODPC的面积.
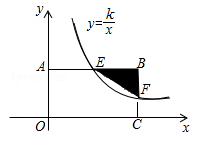
如图,反比例函数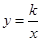 (k>0)的图象与矩形ABCO的两边相交于E,F两点,若E是AB的中点,
(k>0)的图象与矩形ABCO的两边相交于E,F两点,若E是AB的中点,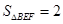 ,则k的值为 .
,则k的值为 .
试题篮
()