如图,在平面直角坐标系中,ΔABC是等腰直角三角形,∠ACB=Rt∠,CA⊥x轴,垂足为点A.点B在反比例函数 的图象上.反比例函数
的图象上.反比例函数 的图象经过点C,交AB于点D,则点D的坐标是 .
的图象经过点C,交AB于点D,则点D的坐标是 .
如图, 中, , 是 的外接圆, 的延长线交边 于点 .
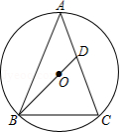
[小题1]求证: ;
[小题2]当 是等腰三角形时,求 的大小;
[小题3]当 , 时,求边 的长.
如图,Rt△ABC中,O为坐标原点,∠AOB=90°,∠B=30°,如果点A在反比例函数 (x>0)的图象上运动,那么点B在函数 (填函数解析式)的图象上运动.
(x>0)的图象上运动,那么点B在函数 (填函数解析式)的图象上运动.
如图,点P是反比例函数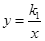 (k1>0,x>0)图象上一动点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交反比例函数
(k1>0,x>0)图象上一动点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交反比例函数 (k2<0且|k2|<k1)的图象于E、F两点.
(k2<0且|k2|<k1)的图象于E、F两点.
(1)图1中,四边形PEOF的面积S1= (用含k1、k2的式子表示);
(2)图2中,设P点坐标为(2,3).
①点E的坐标是( , ) ;点F的坐标是( , )(用含k2的式子表示);
②若△OEF的面积为 ,求反比例函数
,求反比例函数 的解析式.
的解析式.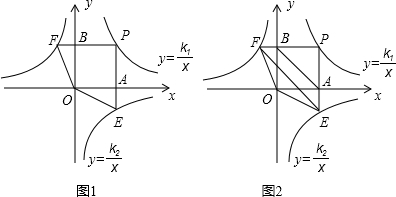
如图,在平面直角坐标系xOy中,抛物线 的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
(1)当m=2时,求点B的坐标;
(2)求DE的长?
(3)①设点D的坐标为(x,y),求y关于x的函数关系式?②过点D作AB的平行线,与第(3)①题确定的函数图象的另一个交点为P,当m为何值时,以,A,B,D,P为顶点的四边形是平行四边形?
(1)如图1,已知△ABC三个顶点的坐标分别为A(1,4)、B(4,1)、C(4,4),若双曲线y= (x>0)与△ABC有公共点,则k的取值范围是 ;
(x>0)与△ABC有公共点,则k的取值范围是 ;
(2)把图1中的△ABC沿直线AB翻折后得到△ABC1,若双曲线y=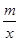 (x>0)与△ABC1有公共点,求m的取值范围;
(x>0)与△ABC1有公共点,求m的取值范围;
小明借助一元二次方程根的判断式圆满地解决了这个问题,小芳借助二次函数模型也圆满地解决了这个问题.请你先在图2中画出△ABC1,再写出自己的解答过程.
(3)如图3,已知点A为(1,2),点B为(4,1),若双曲线y= (x>0)与线段AB有公共点,则n的取值范围是 .
(x>0)与线段AB有公共点,则n的取值范围是 .

如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与反比例函数 的图象相交于点A(m,1)、B(﹣1,n),与x轴相交于点C(2,0),且AC=
的图象相交于点A(m,1)、B(﹣1,n),与x轴相交于点C(2,0),且AC=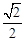 OC.
OC.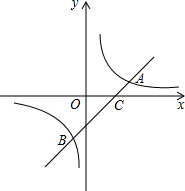
(1)求该反比例函数和一次函数的解析式;
(2)直接写出不等式ax+b≥ 的解集.
的解集.
如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数图象交AB于E点,连接DE。若OD=5,tan∠COD=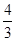 。
。
(1)求过点D的反比例函数的解析式;
(2)求△DBE的面积;
(3)x轴上是否存在点P使△OPD为直角三角形,若存在,请直接写出P点的坐标。若不存在,请说明理由;
问题:如图,在 中, , , , 的平分线 , 分别与直线 交于点 , ,求 的长.
答案: .
探究:(1)把"问题"中的条件" "去掉,其余条件不变.
①当点 与点 重合时,求 的长;
②当点 与点 重合时,求 的长.
(2)把"问题"中的条件" , "去掉,其余条件不变,当点 , , , 相邻两点间的距离相等时,求 的值.
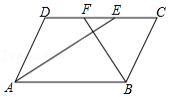
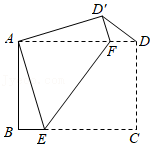
如图,在矩形 中, , ,将此矩形折叠,使点 与点 重合,点 落在点 处,折痕为 ,则 的长为 , 的长为 .
如图, 的直角边 在 轴上,顶点 的坐标为 ,直线 交 于点 ,交 轴于点 .
(1)求直线 的函数表达式;
(2)动点 在 轴上从点 出发,以每秒1个单位的速度向 轴正方向运动,过点 作直线 垂直于 轴,设运动时间为 .
①点 在运动过程中,是否存在某个位置,使得 ,若存在,请求出点 的坐标;若不存在,请说明理由;
②请探索当 为何值时,在直线 上存在点 ,在直线 上存在点 ,使得以 为一边, , , , 为顶点的四边形为菱形,并求出此时 的值.

如图,在平面直角坐标系中,直线l与x轴相交于点M,与y轴相交于点N,Rt△MON的外心为点A(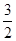 ,-2),反比例函数y=
,-2),反比例函数y= (x>0)的图象过点A.
(x>0)的图象过点A.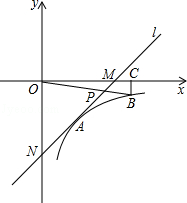
(1)求直线l的解析式;
(2)在函数y= (x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P.若△ONP的面积是△OBC面积的3倍,求点P的坐标.
(x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P.若△ONP的面积是△OBC面积的3倍,求点P的坐标.
如图,在函数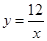 (x>0)的图象上,有点
(x>0)的图象上,有点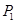 ,
,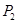 ,
, ,…,
,…,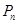 ,
,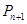 ,若
,若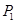 的横坐标为a,且以后每点的横坐标与它前面一个点的横坐标的差都为2,过点
的横坐标为a,且以后每点的横坐标与它前面一个点的横坐标的差都为2,过点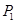 ,
,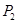 ,
, ,…,
,…,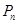 ,
,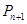 分别作x轴、y轴的垂线段,构成若干个矩形如图所示,将图中阴影部分的面积从左到右依次记为
分别作x轴、y轴的垂线段,构成若干个矩形如图所示,将图中阴影部分的面积从左到右依次记为 ,
,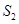 ,
,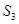 ,…,
,…,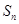 ,则
,则 = ,
= ,  +
+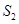 +
+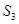 +…+
+…+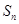 = .(用n的代数式表示)
= .(用n的代数式表示)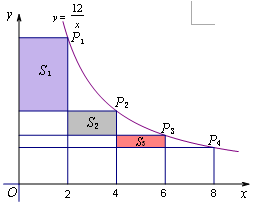
如图1和2,在△ABC中,AB=13,BC=14,cos∠ABC=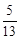 .
.
探究:如图1,AH⊥BC于点H,则AH= ,AC= ,△ABC的面积S△ABC= ;
拓展:如图2,点D在AC上(可与点A,C重合),分别过点A、C作直线BD的垂线,垂足为E,F,设BD=x,AE=m,CF=n(当点D与点A重合时,我们认为S△ABD=0)
(1)用含x,m,n的代数式表示S△ABD及S△CBD;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围.
发现:请你确定一条直线,使得A、B、C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.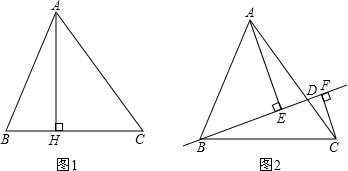
试题篮
()