如图,在矩形 中, , ,将此矩形折叠,使点 与点 重合,点 落在点 处,折痕为 ,则 的长为 , 的长为 .
已知正比例函数y1=x,反比例函数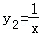 ,由y1,y2构造一个新函数y=x+
,由y1,y2构造一个新函数y=x+ 其图象如图所示.(因其图象似双钩,我们称之为“双钩函数”).给出下列几个命题:
其图象如图所示.(因其图象似双钩,我们称之为“双钩函数”).给出下列几个命题:
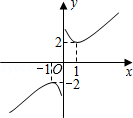
①该函数的图象是中心对称图形;
②当x<0时,该函数在x=﹣1时取得最大值﹣2;
③y的值不可能为1;
④在每个象限内,函数值y随自变量x的增大而增大.
其中正确的命题是 .(请写出所有正确的命题的序号)
在反比例函数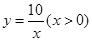 的图象上,有一系列点
的图象上,有一系列点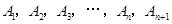 ,若
,若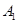 的横坐标为2,且以后每点的横坐标与它前一个点的横坐标的差都为2,现分别过点
的横坐标为2,且以后每点的横坐标与它前一个点的横坐标的差都为2,现分别过点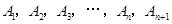 ,作x轴与y轴的垂线段,构成若干个矩形如下图所示,将图中阴影部分的面积从左到右依次记为
,作x轴与y轴的垂线段,构成若干个矩形如下图所示,将图中阴影部分的面积从左到右依次记为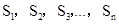 ,则
,则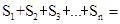 ______.(用n的代数式表示)
______.(用n的代数式表示)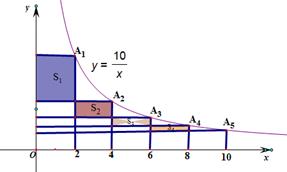
如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(3a,a)是反比例函数y=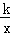 (k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为_________ .
(k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为_________ .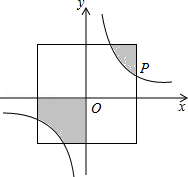
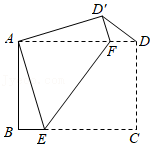
如图,双曲线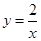 (x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴.将△ABC沿AC翻折后得△AB′C,B′点落在OA上,则四边形OABC的面积是 .
(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴.将△ABC沿AC翻折后得△AB′C,B′点落在OA上,则四边形OABC的面积是 .
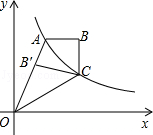
如图,点A在双曲线y=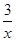 第三象限的分支上,连结AO并延长交第一象限的图象于点B,画BC∥x轴交反比例函数y=
第三象限的分支上,连结AO并延长交第一象限的图象于点B,画BC∥x轴交反比例函数y= 的图象于点C,若△ABC的面积为6,则k的值是 .
的图象于点C,若△ABC的面积为6,则k的值是 .

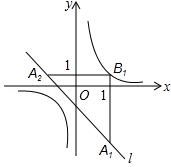
如图,在平面直角坐标系xOy中,已知直线l:y=﹣x﹣1,双曲线y=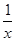 ,在l上取一点A1,过A1作x轴的垂线交双曲线与点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究;过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2013= .
,在l上取一点A1,过A1作x轴的垂线交双曲线与点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究;过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2013= .
如图,点A在双曲线y=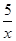 上,点B在双曲线y=
上,点B在双曲线y=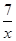 上,且AB∥x轴,C、D在x轴上,若四边形ABCD为平行四边形,则它的面积为 .
上,且AB∥x轴,C、D在x轴上,若四边形ABCD为平行四边形,则它的面积为 .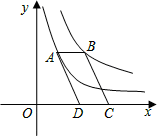
如图,矩形OABC的顶点A,C的坐标分别是(4,0)(0,2),反比例函数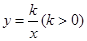 的图像过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则⊿ODE的面积为_____________.
的图像过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则⊿ODE的面积为_____________.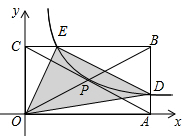
如图,在函数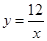 (x>0)的图象上,有点
(x>0)的图象上,有点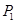 ,
,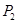 ,
, ,…,
,…,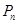 ,
,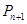 ,若
,若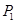 的横坐标为a,且以后每点的横坐标与它前面一个点的横坐标的差都为2,过点
的横坐标为a,且以后每点的横坐标与它前面一个点的横坐标的差都为2,过点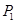 ,
,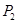 ,
, ,…,
,…,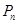 ,
,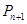 分别作x轴、y轴的垂线段,构成若干个矩形如图所示,将图中阴影部分的面积从左到右依次记为
分别作x轴、y轴的垂线段,构成若干个矩形如图所示,将图中阴影部分的面积从左到右依次记为 ,
,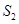 ,
,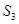 ,…,
,…,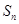 ,则
,则 = ,
= ,  +
+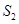 +
+ +…+
+…+ = .(用n的代数式表示)
= .(用n的代数式表示)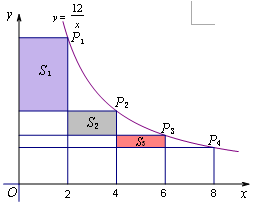
如图,点P是反比例函数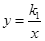 (k1>0,x>0)图象上一动点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交反比例函数
(k1>0,x>0)图象上一动点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交反比例函数 (k2<0且|k2|<k1)的图象于E、F两点.
(k2<0且|k2|<k1)的图象于E、F两点.
(1)图1中,四边形PEOF的面积S1= (用含k1、k2的式子表示);
(2)图2中,设P点坐标为(2,3).
①点E的坐标是( , ) ;点F的坐标是( , )(用含k2的式子表示);
②若△OEF的面积为 ,求反比例函数
,求反比例函数 的解析式.
的解析式.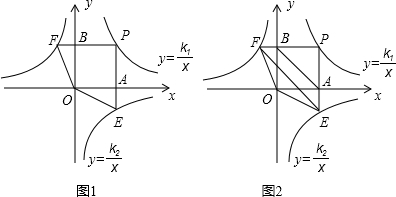
在平面直角坐标系xoy中,对于点P(x,y),其中y≠0,我们把点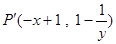 叫做点P的衍生点.已知点
叫做点P的衍生点.已知点 的衍生点为
的衍生点为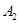 ,点
,点 的衍生点为
的衍生点为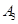 ,点
,点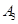 的衍生点为
的衍生点为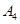 ,…,这样依次得到点
,…,这样依次得到点 ,
,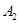 ,
,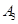 ,…,
,…,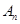 ,…,如果点
,…,如果点 的坐标为(2,-1),那么点
的坐标为(2,-1),那么点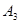 的坐标为________;如果点
的坐标为________;如果点 的坐标为(a,b),且点
的坐标为(a,b),且点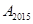 在双曲线y=
在双曲线y=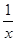 上,那么
上,那么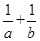 =________.
=________.
试题篮
()