如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC、AC的中点,P是AB上一点,以PF为一直角边作等腰直角三角形PFQ,且∠FPQ=90°,若AB=10,PB=1,则QE的值为( ).

A.3 B.3 C.4 D.4
C.4 D.4
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( ).

| A.1个 | B.2个 | C.3个 | D.4个 |
如图,添加下列一个条件,不能使△ADE∽△ACB的是( ).

| A.DE∥BC | B.∠AED=∠B | C. = = |
D.∠ADE=∠C |
如图,在△ABC中,E、F分别是AB、AC上的点,EF∥BC,且 =
= ,若△AEF的面积为2,则四边形EBCF的面积为( ).
,若△AEF的面积为2,则四边形EBCF的面积为( ).

A.4 B.6 C.16 D.18
下列说法中正确的是( )
| A.位似图形可以通过平移而相互得到 |
| B.位似图形的对应边平行且相等 |
| C.位似图形的位似中心不只有一个 |
| D.位似中心到对应点的距离之比都相等 |
如图,△ABC内接于⊙O,AD⊥BC于点D,BE⊥AC于点E,AD、BE相交于点H.若BC = 6,AH = 4,则⊙O的半径为 ( )

A.5 B.2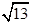 C.
C.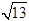 D.5.5
D.5.5
如图, ,∠1=∠2,则对于结论: ①△ABE∽△ACF; ②△ABC∽△AEF ③
,∠1=∠2,则对于结论: ①△ABE∽△ACF; ②△ABC∽△AEF ③ ④
④ ,其中正确的结论的个数是( )
,其中正确的结论的个数是( )

| A.1 | B.2 | C.3 | D.4 |
如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )

A. |
B. |
C. |
D. |
在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )

| A.两人都对 | B.两人都不对 | C.甲对,乙不对 | D.甲不对,乙对 |
试题篮
()