如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒(0<t<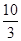 ),连接MN.
),连接MN.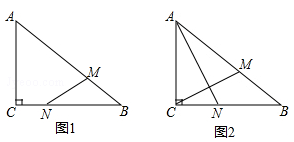
(1)若△BMN与△ABC相似,求t的值;
(2)连接AN,CM,若AN⊥CM,求t的值.
请在图中补全坐标系及缺失的部分,并在横线上写恰当的内容。图中各点坐标如下:A(1,0),B(6,0),C(1,3),D(6,2)。线段AB上有一点M,使△ACM∽△BDM,且相似比不等于1。求出点M的坐标并证明你的结论。
解:M( , )
证明:∵CA⊥AB,DB⊥AB,∴∠CAM=∠DBM= 度。
∵CA=AM=3,DB=BM=2,∴∠ACM=∠AMC( ),∠BDM=∠BMD(同理),
∴∠ACM= (180°- ) =45°。 ∠BDM=45°(同理)。
(180°- ) =45°。 ∠BDM=45°(同理)。
∴∠ACM=∠BDM。
在△ACM与△BDM中, ,
,
∴△ACM∽△BDM(如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似)。
(本小题满分8分)如图,在平行四边形 中,E是AB延长线上的一点,DE交BC于点F.已知
中,E是AB延长线上的一点,DE交BC于点F.已知 ,
, ,求△CDF的面积.
,求△CDF的面积.
如图,已知在△ABC与△DEF中,∠C=54°,∠A=47°,∠F=54°,∠E=79°,
求证:△ABC∽△DEF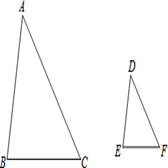
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,点F为线段DE上一点,且∠AFE=∠B.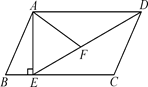
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6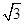 ,AF=4
,AF=4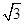 ,求AE的长.
,求AE的长.
如图所示,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以 点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上. 
(1)画出位似中心点O;
(2)直接写出△ABC与△A’B’C’的位似比 ;
(3)以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A′B′C′关于点 O中心对称的△A"B"C",如果△ABC内部一点M的坐标为(x,y),写出△A"B"C"中M的对应点M"的坐标 。
如图,在△ABC中,D为AB边上一点,∠B=∠ACD,[若AD=4,BD=3,求AC的长.
如图,在矩形ABCD中,AB=9,AD=12.动点E从点B出发,沿线段BC(不包括端点B、C)以每秒2个单位长度的速度,匀速向点C运动;动点F从点C出发,沿线段CD(不包括端点C、D)以每秒1个单位长度的速度,匀速向点D运动;点E、F同时出发,同时停止.连接AF并延长交BC的延长线于点M,再把AM沿AD翻折交CD延长线于点N,连接MN.设运动时间为t秒.
(1)当t为何值时,△ABE∽△ECF;
(2)在点E运动的过程中是否存在某个时刻使AE⊥AN?若存在请求出t的值,若不存在请说明理由;
(3)在运动的过程中,△AMN的面积是否变化?如果改变,求出变化的范围;如果不变,求出它的值.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(1)求证: =AB·AD;
=AB·AD;
(2)若AD=4,AB=6,求 的值.
的值.
如图,□ABCD中,E是CD的延长线上一点,BE与AD交于点F,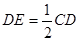 .
.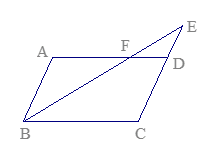
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求□ABCD的面积.
(满分14分)如图,已知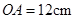 ,
,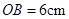 ,点
,点 从点
从点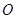 开始沿
开始沿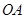 边向点
边向点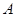 以
以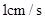 的速度移动,点
的速度移动,点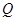 从点
从点 开始向点
开始向点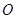 以相同的速度移动,若
以相同的速度移动,若 、
、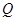 同时出发,移动时间为
同时出发,移动时间为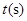 (0≤
(0≤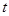 ≤6).
≤6).
(1)设 的面积为
的面积为 ,求
,求 关于
关于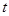 的函数解析式;
的函数解析式;
(2)当 的面积最大时,
的面积最大时, 沿直线
沿直线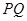 翻折后得到
翻折后得到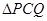 ,试判断点
,试判断点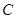 是否落在直线
是否落在直线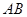 上,并说明理由.
上,并说明理由.
(3)当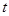 为何值时,
为何值时, 与
与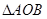 相似.
相似.
试题篮
()