如图,在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从O点开始沿OA边向点A以1cm/s的速度移动,点Q从点B开始沿BO边向点O以1cm/s的速度移动,如果P、Q同时出发,用t(单位:秒)表示移动的时间(0≤t≤6),那么:
(1)当t为何值时,△POQ与△AOB相似?
(2)设△POQ的面积为y,求y关于t的函数关系式.
如图,已知正方形ABCD,点E是边AB上一点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连结OM、ON、BM、BN.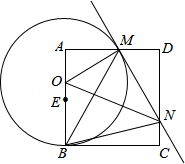
(1)求证:△AOM∽△DMN;
(2)求∠MBN的度数.
如图,AD=2,AC=4,BC=6,∠B=36°,∠D=117°,△ABC∽△DAC.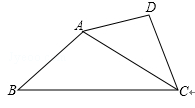
(1)求AB的长;
(2)求CD的长;
(3)求∠BAD的大小.
问题提出
如图①,已知直线l与线段AB平行,试只用直尺作出AB的中点.
初步探索
如图②,在直线l的上方取一个点E,连接EA.EB,分别与l交于点M、N,连接MB.NA,交于点D,再连接ED并延长交AB于点C,则C就是线段AB 的中点.
推理验证
利用图形相似的知识,我们可以推理验证AC=CB.
(1)若线段A.B.C.d长度均不为0,则由下列比例式中,一定可以得出b=d的是
A. B.
B. C.
C. D.
D.
(2)由MN∥AB,可以推出△EFN∽△ECB,△EMN∽△EAB,△MND∽△BAD,△FND∽△CAD.
所以,有 ,
,
所以,AC=CB.
拓展研究
如图③,△ABC中,D是BC的中点,点P在AB上.
(3)在图③中只用直尺作直线l∥BC.
(4)求证:l∥BC.
小明、小亮利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为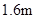 的小明
的小明 的影子
的影子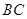 长是
长是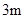 ,而小亮
,而小亮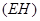 刚好在路灯灯泡的正下方
刚好在路灯灯泡的正下方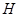 点,并测得
点,并测得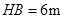 .
.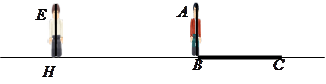
(1)请在图中画出形成影子的光线,交确定路灯灯泡所在的位置 ;
;
(2)求路灯灯泡的垂直高度 .
.
(本题10分)如图13-1,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为 米.
米.
(1)用含 的式子表示花圃的面积;
的式子表示花圃的面积;
(2)如果通道所占面积是整个长方形空地面积的 ,求出此时通道的宽;
,求出此时通道的宽;
(3)若按上述要求施工,同时校长希望长方形花圃的形状与原长方形空地的形状相似,聪明的你想一想能不能满足校长的要求,若能,求出此时通道的宽;若不能,则说明理由。
已知在△ABC中,∠B=90o,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
(1)求证:AC·AD=AB·AE;
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒(0<t<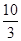 ),连接MN.
),连接MN.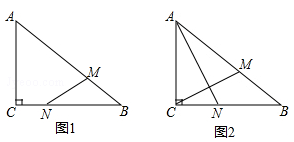
(1)若△BMN与△ABC相似,求t的值;
(2)连接AN,CM,若AN⊥CM,求t的值.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,点F为线段DE上一点,且∠AFE=∠B.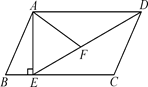
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6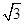 ,AF=4
,AF=4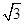 ,求AE的长.
,求AE的长.
如图,在矩形ABCD中,AB=9,AD=12.动点E从点B出发,沿线段BC(不包括端点B、C)以每秒2个单位长度的速度,匀速向点C运动;动点F从点C出发,沿线段CD(不包括端点C、D)以每秒1个单位长度的速度,匀速向点D运动;点E、F同时出发,同时停止.连接AF并延长交BC的延长线于点M,再把AM沿AD翻折交CD延长线于点N,连接MN.设运动时间为t秒.
(1)当t为何值时,△ABE∽△ECF;
(2)在点E运动的过程中是否存在某个时刻使AE⊥AN?若存在请求出t的值,若不存在请说明理由;
(3)在运动的过程中,△AMN的面积是否变化?如果改变,求出变化的范围;如果不变,求出它的值.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(1)求证: =AB·AD;
=AB·AD;
(2)若AD=4,AB=6,求 的值.
的值.
如图,□ABCD中,E是CD的延长线上一点,BE与AD交于点F,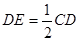 .
.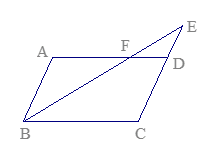
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求□ABCD的面积.
试题篮
()