如图,梯形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点。EF与BD相交于点M.
(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.
小明、小亮利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为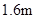 的小明
的小明 的影子
的影子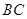 长是
长是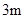 ,而小亮
,而小亮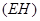 刚好在路灯灯泡的正下方
刚好在路灯灯泡的正下方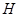 点,并测得
点,并测得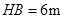 .
.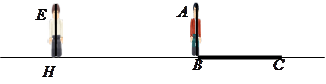
(1)请在图中画出形成影子的光线,交确定路灯灯泡所在的位置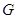 ;
;
(2)求路灯灯泡的垂直高度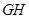 .
.
已知:如图,在△ABC中,D,E分别是AB,AC上一点,且∠AED =∠B.若AE=5,AB=9,CB=6.
(1)求证:△ADE∽△ACB;(2)求ED的长.
已知如图, 是△
是△ 的边
的边 上一点,
上一点, ∥
∥ ,交边
,交边 于点
于点 ,延长
,延长 至点
至点 ,使
,使 ,联结
,联结 ,交边
,交边 于点
于点 ,联结
,联结

(1)求证: ;
;
(2)如果 ,求证:
,求证:
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°.
(1)求证:△ABD∽△DCE;
(2)若BD=3,CE=2,求△ABC的边长.
(本题10分)如图13-1,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为 米.
米.
(1)用含 的式子表示花圃的面积;
的式子表示花圃的面积;
(2)如果通道所占面积是整个长方形空地面积的 ,求出此时通道的宽;
,求出此时通道的宽;
(3)若按上述要求施工,同时校长希望长方形花圃的形状与原长方形空地的形状相似,聪明的你想一想能不能满足校长的要求,若能,求出此时通道的宽;若不能,则说明理由。
如图,在正方形 中,
中, 分别是边
分别是边 上的点,
上的点, 连结
连结 并延长交
并延长交 的延长线于点
的延长线于点

(1)求证: ;
;
(2)若正方形ABCD的边长为8,求 的长.
的长.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(1)求证: =AB·AD;
=AB·AD;
(2)若AD=4,AB=6,求 的值.
的值.
如图,□ABCD中,E是CD的延长线上一点,BE与AD交于点F,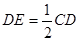 .
.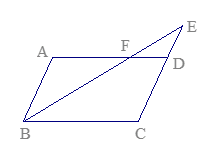
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求□ABCD的面积.
(满分14分)如图,已知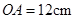 ,
,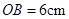 ,点
,点 从点
从点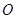 开始沿
开始沿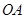 边向点
边向点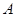 以
以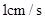 的速度移动,点
的速度移动,点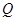 从点
从点 开始向点
开始向点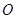 以相同的速度移动,若
以相同的速度移动,若 、
、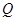 同时出发,移动时间为
同时出发,移动时间为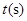 (0≤
(0≤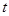 ≤6).
≤6).
(1)设 的面积为
的面积为 ,求
,求 关于
关于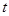 的函数解析式;
的函数解析式;
(2)当 的面积最大时,
的面积最大时, 沿直线
沿直线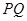 翻折后得到
翻折后得到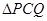 ,试判断点
,试判断点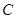 是否落在直线
是否落在直线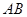 上,并说明理由.
上,并说明理由.
(3)当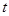 为何值时,
为何值时, 与
与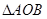 相似.
相似.
试题篮
()