小强想利用树影测树高,他在某一时刻测得直立的标杆长0.8m,其影长为1m,同时测树影时因树靠近某建筑物,影子不全落在地上,有一部分落在墙上如图,若此时树在地面上的影长为5.5m,在墙上的影长为1.5m,求树高
如图,在 的正方形网格中,△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
的正方形网格中,△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
(1)以点O(0,0)为位似中心,按比例尺(OA︰OA’)1:3在位似中心的同侧将△OAB放大为△OA’B’,放大后点A、B的对应点分别为A’、B’ .画出△OA’B’,并写出点A’、B’的坐标:A’( ),B’( );
(2)在(1)中,若 为线段
为线段 上任一点,写出变化后点
上任一点,写出变化后点 的对应点
的对应点 的坐标( ).
的坐标( ).
如图,一条小“鱼”的头部点O的坐标为(0,0),其鱼鳍部位点A的坐标为(3,2).请以点O为位似中心,在方格中画出一条大鱼与小鱼成位似图形,且位似比为2;
在你所画的图中找出与点A对应的点,记为A’,则点A’的坐标为____________.
两个立体图形的体积比是其相似比的立方,如两个立方体的体积之比为两立方体棱长之比的立方.根据这个结论可知:若小鱼的质量为1kg,则大鱼的质量大约为_________kg.

如本题图1,在 中,
中, 、
、 、
、 分别为三边的中点,
分别为三边的中点, 点在边
点在边 上,
上, 与四边形
与四边形 的周长相等,设
的周长相等,设 、
、 、
、 .
.
(1)求线段 的长(用含
的长(用含 、
、 、
、 的代数式表示);
的代数式表示);
(2)求证: 平分
平分 ;
;
(3)连接 ,如本题图2,若
,如本题图2,若 与
与 相似,求证:
相似,求证: .
.
如图22,在12×12的正方形网格中,△TAB 的顶点坐标T(1,1)、A(2,3)、B(4,2).以点T(1,1)为位似中心,按比例尺(TA′∶TA)3∶1,并在位似中心的同侧,将△TAB放大为△TA′B′,放大后点A、B的对应点分别为A′、B′.画出△TA′B′,并写出点A′、B′的坐标;
在(1)中,若C(a,b)为线段AB上任意一点,写出变化后C的对应点
C′的坐标.
如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(1)求证: =AB·AD;
=AB·AD;
(2)若AD=4,AB=6,求 的值.
的值.
如图,□ABCD中,E是CD的延长线上一点,BE与AD交于点F,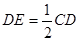 .
.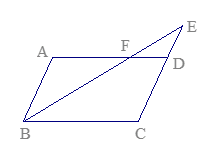
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求□ABCD的面积.
(满分14分)如图,已知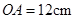 ,
,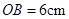 ,点
,点 从点
从点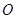 开始沿
开始沿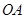 边向点
边向点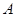 以
以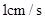 的速度移动,点
的速度移动,点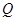 从点
从点 开始向点
开始向点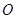 以相同的速度移动,若
以相同的速度移动,若 、
、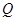 同时出发,移动时间为
同时出发,移动时间为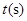 (0≤
(0≤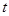 ≤6).
≤6).
(1)设 的面积为
的面积为 ,求
,求 关于
关于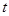 的函数解析式;
的函数解析式;
(2)当 的面积最大时,
的面积最大时, 沿直线
沿直线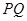 翻折后得到
翻折后得到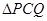 ,试判断点
,试判断点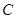 是否落在直线
是否落在直线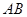 上,并说明理由.
上,并说明理由.
(3)当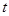 为何值时,
为何值时, 与
与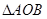 相似.
相似.
已知:ΔABC在坐标平面内,三个顶点的坐标为A(0,3)、B(3,4)、C(2,2),(正方形网格中,每个小正方形边长为1个单位长度)
(1)画出ΔABC向下平移4个单位得到的ΔA1B1C1。
(2)以B为位似中心,在网格中画出ΔA2BC2,使ΔA2BC2与ΔABC位似,且位似比2 :1,直接写出C2点坐标是 。
(3)ΔA2BC2的面积是 平方单位。
如图,在□ABCD中,过点B作BE⊥CD,垂足为E,连接AE.F为AE上一点,且∠BFE=∠C.
⑴试说明:△ABF∽△EAD;
⑵若AB=8,BE=6,AD=7,求BF的长.
试题篮
()