初中数学相似多边形的性质解答题

如图，AD和CB相交于点O，且AB∥CD，OA=OB．求证：OC=OD．

如图，四边形ABCD中，AC平分∠DAB，∠ADC＝∠ACB＝90°， E为AB中点，

（1）求证：AC²＝AB•AD；
（2）若AD＝4，AB＝6，求的值．

如图，在边长为1的正方形网格中，有一格点△ABC，已知A、B、C三点的坐标分别是A（1，0）、B（2，－1）、C（3，1）．
 
（1）请在网格图形中画出平面直角坐标系；
（2）以原点O为位似中心，将△ABC放大2倍，画出放大后的△A′B′C′；
（3）写出△A′B′C′各顶点的坐标：A′____，B′____，C′  ___；

如图，四边形ABCD中，AC平分∠DAB，∠ADC=∠ACB=90°，E为AB中点，

（1）求证：AC²=AB•AD；
（2）若AD=4，AB=6，求的值．

如图，在边长为1的正方形网格中，有一格点△ABC，已知A、B、C三点的坐标分别是A（1，0）、B（2，－1）、C（3，1）．

（1）请在网格图形中画出平面直角坐标系；
（2）以原点O为位似中心，将△ABC放大2倍，画出放大后的△A′B′C′；
（3）写出△A′B′C′各顶点的坐标：A′____，B′____，C′  ___；

如图，∠ACB＝∠ADC＝90°，AC＝，AD＝2．问当AB的长为多少时，这两个直角三角形相似？

如图，，试求和的值．（4+4）

（本题共8分）阅读下列材料：小昊遇到这样一个问题：如图1，在△ABC中，∠ACB=90°，BE是AC边上的中线，点D在BC边上，CD：BD=1：2，AD与BE相交于点P，求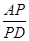的值．
小昊发现，过点A作AF∥BC，交BE的延长线于点F，通过构造△AEF，经过推理和计算能够使问题得到解决（如图2）．请回答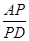：的值为__________．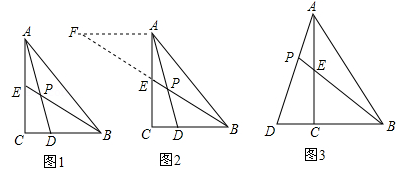

参考小昊思考问题的方法，解决问题：
如图 3，在△ABC中，∠ACB=90°，点D在BC的延长线上，AD与AC边上的中线BE的延长线交于点P，DC：BC：AC=1：2：3 ．
（1）求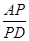的值；
（2）若CD=2，则BP=_________________．

（本题共6分）如图，在Rt△ABC中，∠C=90°，△ACD沿AD折叠，使得点C落在斜边AB上的点E处．

（1）求证：△BDE∽△BAC；
（2）已知AC=6，BC=8，求线段AD的长度．

（本题共6分）如图，每个小方格都是边长为1个单位的小正方形，A．B．C三点都是格点（每个小方格的顶点叫格点），其中A（1，8），B（3，8），C（4，7）．

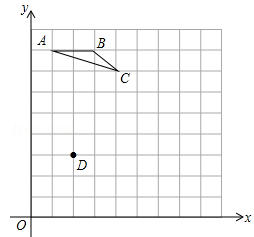
（1）若D（2，3），请在网格图中画一个格点△DEF，使△DEF ∽△ABC，且相似比为2∶1；
（2）求△ABC中AC边上的高；
（3）若△ABC外接圆的圆心为P，则点P的坐标为          ．

如图，在Rt△ABC中∠ACB=90°，CD⊥AB于D ．已知AC=6,AD=2求AB？

如图，已知AB⊥BD，CD⊥BD．

（1）若AB＝16，CD＝9，BD＝15，请问在BD上是否存在P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似？若存在，求BP的长；若不存在，请说明理由；
（2）若AB＝16，CD＝9，BD＝24，请问在BD上存在多少个P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似？并求BP的长；
（3）若AB＝m，CD＝n，BD＝，请问在m、n、满足什么关系时，存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的三个P点?

（本小题满分6分）如图，△ABC中，CD是边AB上的高，且．

（1）求证：△ACD∽△CBD；
（2）求∠ACB的大小．

（本小题满分6分）如图，在边长为1个单位长、度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）．

（1）将△ABC向左平移1个单位，再向上平移5个单位得到△A₁B₁C₁，请画出△A₁B₁C₁；
（2）请在网格中将△ABC以A为位似中心放大 3倍，得△AB₂C₂，请画出△AB₂C₂

如图，以等腰三角形的一腰为直径的⊙O交底边于点，交于点，连结，并过点作，垂足为．根据以上条件写出三个正确结论（除外）是：

（1）___________________________________________________________________________；
（2）___________________________________________________________________________；
（3）___________________________________________________________________________．