初中数学相似多边形的性质解答题

如图，在平面直角坐标系中，点O为坐标原点，以点A（0，-3）为圆心，5为半径作圆A，交x轴于B、C两点，交y轴于点D、E两点．

（1）如果一个二次函数图象经过B、C、D三点，求这个二次函数的解析式；
（2）设点P的坐标为（m,0）(m>5),过点P作x轴交（1）中的抛物线于点Q，当以为顶点的三角形与相似时，求点P的坐标．

(本题满分12分）正方形边长为4，、分别是、上的两个动点，当点在上运动时，保持和垂直，

⑴证明：；
⑵设，梯形的面积为，求与之间的函数关系式；
⑶梯形的面积可能等于12吗？为什么？

如图，在等腰梯形中，∥，AD=AB.过作，交于，延长至，使.
 
（1）请指出四边形的形状，并证明；
（2）如果，，求三角形的面积.

如右图，在等腰梯形ABCD中，AD∥BC，AD=AB.过A作AF⊥BD，交BC于G，延长BC至E，使CE=CD.
（1）请指出四边形ACED的形状，并证明；
（2）如果BD=8，AG=6，求△BDE的面积.

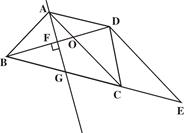
如右图，路灯A离地8米，身高1.6米的小王（C D）的影长DB与身高一样，现在他沿OD方向走10米，到达E处.
（1）请画出小王在E处的影子EH；
（2）求EH的长.

如图，在中，，是斜边上的中线，，，点是延长线上的一动点，过点作，交延长线于点，
设．

（1）求关于的函数关系式及定义域；
（2）联结，当平分时，求的长；
（3）过点作交于，当和相似时，求的值．

如图，的顶点A、B在二次函数的图像上，又点A、B[来分别在轴和轴上，∠ABO＝．

（1）求此二次函数的解析式；

（2）过点作∥交上述函数图像于点，

点 在上述函数图像上，当 与 相似时，求点 的坐标．

（本题满分12分）
如图，梯形中，∥，，点在边上，与相交于点，且．

求证：（1）∽；   
（2）．

如图，在中，点在边上，点在边上，且∥，．

（1）求证：∥；
（2）如果，，求的值．

如图，□中，∥，∥，点是的中点，和相交于点．

（1）求的值；
（2）如果，，请用、表示   

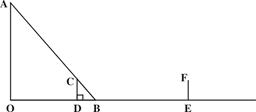
（本题满分14分，其中第（1）、（2）小题各4分，第（3）小题6分）已知：如图，在平面直角坐标系xOy中，二次函数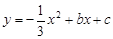的图像经过点A（-1,1）和点B（2,2），该函数图像的对称轴与直线OA、OB分别交于点C和点D．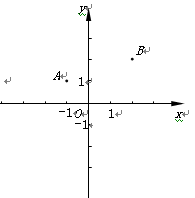

（1）求这个二次函数的解析式和它的对称轴；
（2）求证：∠ABO=∠CBO；
（3）如果点P在直线AB上，且△POB
与△BCD相似，求点P的坐标．

（本题满分12分，其中第（1）小题5分，第（2）小题7分）
已知：如图，在△ABC中，AD是边BC上的中线，点E在线段BD上，且BE=ED，过点B作BF∥AC，交线段AE的延长线于点F．

（1）求证：AC=3BF；
（2）如果，求证：．

已知：如图，矩形DEFG的一边DE在△ABC的边BC上，顶点G、F分别在边AB、AC上，AH是边BC上的高，AH与GF相交于点K，已知BC=12，AH=6，EF∶GF=1∶2，求矩形DEFG的周长．

在Rt△ABC中，∠ACB=90，AC=BC，CD⊥AB于点D，点E为AC边上一点，联结BE交CD于点F，过点E作EG⊥BE交AB于点G，
如图1，当点E为AC中点时，线段EF与EG的数量关系是        ；
如图2，当，探究线段EF与EG的数量关系并且证明；
如图3，当，线段EF与EG的数量关系是        ．

小明喜欢研究问题，他将一把三角板的直角顶点放在平面直角坐标系的原点处，两条直角边与抛物线交于、两点．
（1）如左图，当时，则=          ；

（2）对同一条抛物线，当小明将三角板绕点旋转到如右图所示的位置时，过点作轴于点，测得，求出此时点的坐标；

（3）对于同一条抛物线，当小明将三角板绕点旋转任意角度时，他惊奇地发现，若三角板的两条直角边与抛物线有交点，则线段总经过一个定点，请直接写出该定点的坐标．