在图①至图③中,△ABC为直角三角形,且∠ABC=90º,∠A=30º,点P在AC上,∠MPN=90º.



当点P为线段AC的中点,点M、N分别在线段AB、BC上,且PM⊥AB,
PN⊥BC(如图①)时,则PN和PM的数量关系是:PN=________PM;
当点P为线段AC的中点,点M、N分别在线段AB、BC上(如图②)时,求
 的值
的值
当PC=PA,点M、N分别在线段AB、BC上(如图③)时,求
 的值;
的值;
如图①,梯形ABCD中,DC∥AB,DE⊥AB于点E.
阅读理解:
在图①中,延长梯形ABCD的两腰AD、BC交于点P,过点D作DF∥CB交AB于点F,得到图②;四边形BCDF的面积为 ,△ADF的面积
,△ADF的面积 ,△PDC的面积
,△PDC的面积 .
.
在图②中,若DC=2,AB=8,DE=3,则
 ,
, ______,
______, ;
;在图②中,若
 ,
, ,
, ,则
,则 =__________,并写出理由;
=__________,并写出理由;如图③,□DEFC的四个顶点在△PAB的三边上,若△PDC、△ADE、△CFB的面积分别为2、3、5,试利用(2)中的结论求△PAB的面积.

在边长为10的正方形ABCD中,以AB为直径作半圆O,如图①,E是半圆上一动点,过点E作EF⊥AB,垂足为F,连结DE.
当DE=10时,求证:DE与圆O相切;
求DE的最长距离和最短距离;
如图②,建立平面直角坐标系,当DE =10时,试求直线DE的解析式.
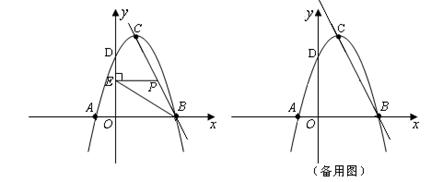
如图,在直角坐标系中,抛物线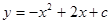 与
与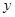 轴交于点D(0,3).
轴交于点D(0,3).
直接写出
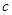 的值;
的值;
若抛物线与
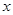 轴交于A、B两点(点B在点A的右边),顶点为C点,求直线BC的解析式;
轴交于A、B两点(点B在点A的右边),顶点为C点,求直线BC的解析式;
已知点P是直线BC上一个动点,
①当点P在线段BC上运动时(点P不与B、C重合),过点P作PE⊥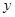 轴,垂足为E,连结BE.设点P的坐标为(
轴,垂足为E,连结BE.设点P的坐标为(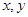 ),△PBE的面积为
),△PBE的面积为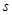 ,求
,求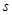 与
与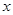 的函数关系式,写出自变量
的函数关系式,写出自变量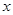 的取值范围,并求出
的取值范围,并求出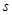 的最大值;
的最大值;
②试探索:在直线BC上是否存在着点P,使得以点P为圆心,半径为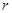 的⊙P,既与抛物线的对称轴相切,又与以点C为圆心,半径为1的⊙C相切?如果存在,试求
的⊙P,既与抛物线的对称轴相切,又与以点C为圆心,半径为1的⊙C相切?如果存在,试求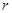 的值,并直接写出点P的坐标;如果不存在,请说明理由.
的值,并直接写出点P的坐标;如果不存在,请说明理由.
在平面直角坐标系中△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆过点C,若C的坐标为(0,2),AB="5," A,B两点的横坐标XA,XB是关于X的方程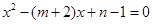 的两根:
的两根:
求m,n的值;
若∠ACB的平分线所在的直线
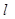 交x轴于点D,试求直线
交x轴于点D,试求直线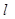 对应的一次函数的解析式;
对应的一次函数的解析式;过点D任作一直线
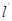 分别交射线CA,CB(点C除外)于点M,N,则
分别交射线CA,CB(点C除外)于点M,N,则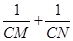 的值是否为定值,若是,求出定值,若不是,请说明理由
的值是否为定值,若是,求出定值,若不是,请说明理由
已知:如图①,在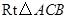 中,
中,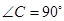 ,
,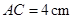 ,
,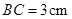 ,点
,点 由
由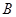 出发沿
出发沿 方向向点
方向向点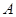 匀速运动,速度为1cm/s;点
匀速运动,速度为1cm/s;点 由
由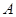 出发沿
出发沿 方向向点
方向向点 匀速运动,速度为2cm/s;连接
匀速运动,速度为2cm/s;连接 .若设运动的时间为
.若设运动的时间为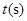 (
( ),解答下列问题
),解答下列问题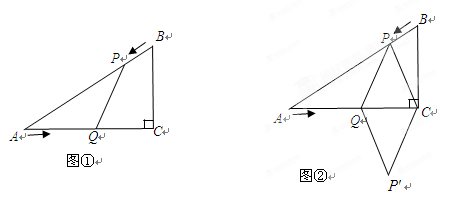
当
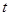 为何值时,
为何值时,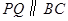 ?
?设
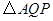 的面积为
的面积为 (
(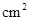 ),求
),求 与
与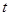 之间的函数关系式;
之间的函数关系式;是否存在某一时刻
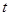 ,使线段
,使线段 恰好把
恰好把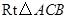 的周长和面积同时平分?若存在,求出此时
的周长和面积同时平分?若存在,求出此时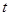 的值;若不存在,说明理由;
的值;若不存在,说明理由;如图②,连接
 ,并把
,并把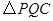 沿
沿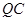 翻折,得到四边形
翻折,得到四边形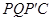 ,那么是否存在某一时刻
,那么是否存在某一时刻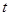 ,使四边形
,使四边形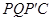 为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
正方形ABCD中,点P是AD上的一动点(与点D、点A不重合),DE⊥CP,垂足为E,EF⊥BE与DC交于点F.
求证:△DEF∽△CEB;
当点P运动到DA的中点时,求证:点F为DC的中点.
在图11的方格纸中,△OAB的顶点坐标分别为O(0,0)、A(-2,-1)、B(-1,-3),△O1A1B1与△OAB是关于点P为位似中心的位似图形.
在图中标出位似中心P的位置,并写出点P及点B的对应点B1的坐标;
以原点O为位似中心,在位似中心的同侧画出△OAB的一个位似△OA2B2,使它与△OAB的相似比为2:1. 并写出点B的对应点B2的坐标;
△OAB内部一点M的坐标为(a,b),写出M在△OA2B2中的对应点M2的坐标
判断△OA2B2能否看作是由△O1A1B1经过某种变换后得到的图形,若是,请指出是怎样变换得到的(直接写答案)
、(本题12分)如图,设抛物线C1: , C2:
, C2: ,C1与C2的交点为A, B,点A的坐标是
,C1与C2的交点为A, B,点A的坐标是 ,点B的横坐标是-2.
,点B的横坐标是-2.
(1)求
 的值及点B的坐标;
的值及点B的坐标; (2)点D在线段AB上,过D作x轴的垂线,垂足为点H,在DH的右侧作正三角形DHG.记过C2顶点M的直线为
 ,且
,且 与x轴交于点N.
与x轴交于点N.
① 若 过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
② 若 与△DHG的边DG相交,求点N的横坐标的取值范围.
与△DHG的边DG相交,求点N的横坐标的取值范围.
(本小题满分14分)
如图,已知抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3)。设抛物线的顶点为D,求解下列问题:

(1)求抛物线的解析式和D点的坐标;
(2)过点D作DF∥
 轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
(3)能否在抛物线上找到一点Q,使△BDQ为直角三角形?若能找到,试写出Q点的坐标;若不能,请说明理由。
.(本小题满分12分)
如图,已知在⊙O中,直径AB=10,点E是OA上任意一点,过E作弦CD⊥AB,点F是弧BC上一点,连结AF交CE于H,连结AC、CF、BF。
(1)请你找出图中的相似三角形,并对其中的一对相似三角形进行证明;
(2)若AE:BE=1:4,求CD长。
(3)在(2)的条件下,求
 的值。
的值。
在矩形ABCD中,AB=4,BC=10,点M在BC上。
(1)若BM=3时,求点D到直线AM的距离;
(2)若AM⊥DM,求BM的长。
(本小题满分10分)如图,在平面直角坐标系中,点A、B、C、P的坐标分别为(0,1)、(-1,0)、(1,0)、(-1,-1)。
(1)求经过A、B、C三点的抛物线的表达式;
(2)以P为位似中心,将△ABC放大,使得放大后的△A1B1C1
与△OAB对应线段的比为3:1,请在右图网格中画出放大
后的△A1B1C1;(所画△A1B1C1与△ABC在点P同侧);(3)经过A1、B1、C1三点的抛物线能否由(1)中的抛物线平
移得到?请说明理由。
(本小题满分6分)如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE。
(1)写出图中两对相似三角形(不得添加辅助线);
(2)请分别说明两对三角形相似的理由。
试题篮
()