初中数学相似多边形的性质解答题

（本小题满分14分）
在如图所示的一张矩形纸片（）中，将纸片折叠一次，使点与重合，再展开，折痕交边于，交边于，分别连结和．

（1）求证：四边形是菱形；
（2）过作交于，求证：
（3）若，的面积为，求的周长；

如图1，边长为2的正方形ABCD中，E是BA延长线上一点，且AE＝AB，点P从点D
出发，以每秒1个单位长度沿D→C→B向终点B运动，直线EP交AD于点F，过点F作
直线FG⊥DE于点G，交AB于点R。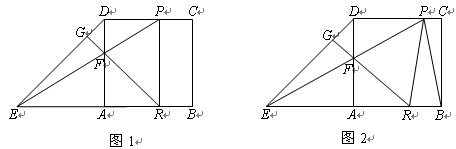

（1）求证：AF＝AR；
（2）设点P运动的时间为t，
①求当t为何值时，四边形PRBC是矩形？
②如图2，连接PB。请直接写出使△PRB是等腰三角形时t的值。

如图1，在△ABC中，AB＝BC＝5，AC="6." △ECD是△ABC沿CB方向平移得到的，连结AE，AC和BE相交于点O.

（1）判断四边形ABCE是怎样的四边形，并证明你的结论；
（2）如图2，P是线段BC上一动点（不与点B、C重合），连接PO并延长交线段AE于点Q，QR⊥BD，垂足为点R.
①四边形PQED的面积是否随点P的运动而发生变化？若变化，请说明理由；若不变，求出四边形PQED的面积；
②当线段BP的长为何值时，以点P、Q、R为顶点的三角形与△BOC相似？

已知，延长BC到D，使．取的中点，连结交于点．

求的值
若，求的长

如图，在Rt△ABC中，∠ACB=90º，AB=10，AC=6，点E、F分别是边AC、BC上的动点，过点E作ED⊥AB于点D，过点F作FG⊥AB于点G，DG的长始终为2．
当AD=3时，求DE的长；
当点E、F在边AC、BC上移动时，设，，
求关于的函数解析式，并写出函数的定义域；
在点E、F移动过程中，△AED与△CEF能否相似，
若能，求AD的长；若不能，请说明理由．

如图，已知△ABC中CEAB于E，BFAC于F，
求证：△AFE～△ABC
若时，若∠A=60°,求△AFE与△ABC面积之比。

如图，四边形ABCD是正方形，CE是∠BCD的外角∠DCF的平分线．

（如果需要，还可以继续操作、实验与测量）
操作实验：将直角尺的直角顶点P在边BC上移动（与点B、C不重合），且一直角边经过点A，另一直角边与射线CE交于点Q，不断移动P点，同时测量线段PQ与线段PA的长度，完成下列表格（精确到0.1cm）．

	PA	PQ
第一次
第二次

 
观测测量结果，猜测它们之间的关系：____________
请证明你猜测的结论；
当点P在BC的延长线上移动时，继续⑴的操作实验，试问：⑴中的猜测结论还成立吗？若成立，请给出证明；若不成立，请说明理由．
（考查猜想、证明等综合能力）

王华同学在晚上由路灯AC走向路灯BD，当他走到点P时，发现身后他影子的顶部刚好接触到路灯AC的底部，当他向前再步行12m到达Q点时，发现身前他影子的顶部刚好接触到路灯BD的底部.已知王华同学的身高是1.6m，两个路灯的高度都是9.6m.

求两个路灯之间的距离；（考查投影及相似三角形中的比例计算）
当王华同学走到路灯BD处时，他在路灯AC下的影子长是多少？

如图,△ABC中,AB=AC,过点A作GE∥BC,角平分线BD、CF相交于点H,它们的延长线分别交GE于点E、G.试在图中找出3对全等三角形,并对其中一对全等三角形给出证明.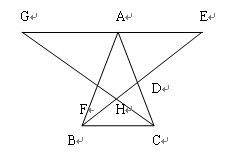

已知：AB是⊙O的直径，弦CD⊥AB于点G，E是直线AB上一动点（不与点A、B、G重合），直线DE交⊙O于点F，直线CF交直线AB于点P.设⊙O的半径为r.
（1）如图1，当点E在直径AB上时，试证明：OE·OP＝r²
（2）当点E在AB（或BA）的延长线上时，以如图2点E的位置为例，请你画出符合题意的图形，标注上字母，（1）中的结论是否成立？请说明理由.
 

(本题8分)如图，在一块三角形区域ABC中，∠C=90°，边AC=8m，BC=6m，现要在△ABC内建造一个矩形水池DEFG，如图的设计方案是使DE在AB上．

（1）求△ABC中AB边上的高h；
（2）设DG=x，水池DEFG的面积为S，求S关于x的函数关系式，当x取何值时，水池DEFG的面积S最大？

（本题12分）如图，抛物线经过的三个顶点，已知轴，点在轴上，点在轴上，且．

（1）求抛物线的对称轴；
（2）写出A，B，C三点的坐标（A，B，C三点的坐标只需写出答案），并求抛物线的解析式；
（3）探究：若点是抛物线对称轴上且在轴下方的动点，是否存在是等腰三角形．若存在，求出所有符合条件的点坐标；不存在，请说明理由．

（本题12分）AB是⊙O的直径，点E是半圆上一动点（点E与点A、B都不重合），点C是BE延长线上的一点，且CD⊥AB，垂足为D，CD与AE交于点H，点H与点A不重合。

（1）求证：△AHD∽△CBD
（2）若CD=AB=2，求HD+HO的值。

如图，在△ABC中，AB=AC，以AB为直径的⊙O交AC与E，交BC与D．求证：

（1）D是BC的中点；（2）△BEC∽△ADC；（3）BC²=2AB·CE．

（本题8分）如图，在Rt△ABC中，AC=4，BC=3．在Rt△ABC内并排放入（不重叠）n个小正方形纸片，使这些纸片的一边都在AB上，首尾两个正方形各有一个顶点D、E分别在AC、BC上，求小正方形的边长（用n的代数式表示）。