初中数学相似多边形的性质解答题

如图测量电线杆AB的高度，发现电线杆的影子恰好落在土坡的坡面CD和地面BC上，量得CD="4" m，BC="10" m，CD与地面成30°角，且此时测得1m杆的影子长为2 m，则电线杆的高度约为多少m？

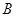（1）请在方格纸上建立平面直角坐标系，使，并求出点坐标；
（2）以原点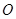为位似中心，相似比为2：1，在第一象限内将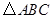放大，画出放大后的图形；

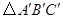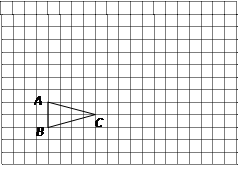
已知：等腰梯形ABCD，AD∥BC,AB=DC=5,AD=6,BC=12,动点P从点D出发沿DC以每秒1个单位向终点C运动，点Q从点C出发沿CB以每秒2个单位向B运动，当点P到达C时，点Q随之停止运动，设点P运动的时间为t秒.

（1）求梯形ABCD面积.
（2）当PQ∥AB时，求t.
（3） 当点P、Q、C三点构RT△时，求t值.

如图，已知每个小方格都是边长为1的正方形，我们称每个小正方形的顶点为格点，以格点为顶点的图形称为格点图形. 图中的△ABC是一个格点三角形.

请你在第一象限内画出格点△AB₁C₁，使得△AB₁C₁∽△ABC，且△AB₁C₁与△ABC的相似比为3：1；
写出B₁、C₁两点的坐标.

为了测量学校操场上旗杆的高度，小明请同学帮忙，测量了同一时刻自己的影长EC和旗杆的影长BC分别为0.6m和3.6m，如图，如果小身高CD为1.5m，请计算旗杆AB的高度。

 如图，在矩形ABCD中，，，点P沿AB边从点A开始向B以2cm/s的速度移动；点Q沿DA边从点D开始向点A以1cm/s的速度移动。如果P、Q同时出发，用t（秒）表示移动的时间，那么当t为何值时，以点Q、A、P为顶点的三角形与相似？

(本题满分11分)
如图（1），已知正方形ABCD在直线MN的上方，BC在直线MN上，E是BC上一点，以AE为边在直线MN的上方作正方形AEFG．
（1）连接GD，求证：△ADG≌△ABE；(2分)
（2）连接FC，观察并猜测∠FCN的度数，并说明理由；(3分)
（3）如图（2），将图（1）中正方形ABCD改为矩形ABCD，AB=a，BC=b（a、b为常数），E是线段BC上一动点（不含端点B、C），以AE为边在直线MN的上方作矩形AEFG，使顶点G恰好落在射线CD上．判断当点E由B向C运动时，∠FCN的大小是否总保持不变，若∠FCN的大小不变，请用含a、b的代数式表示tan∠FCN的值；若∠FCN的大小发生改变，请举例说明．(4分)

如图1，在平面直角坐标系xoy中，Rt△AOB的斜边OB在x轴上，其中∠ABO=30°，OB=4。

⑴直接写出，Rt_△AOB的内心和P的坐标；
⑵如图2，若将Rt_△AOB绕其直角顶点A顺时针旋转α度（0°<α<90°），得到Rt_△ACD，直角边AD与x轴相交于点N，直角边AC与y轴相交于点M，连结MN。设△MON的面积为S_△MON，△AOB的面积为S_△AOB，以点M为圆心，MO为半径作⊙M，
①当直线AD与⊙M相切时，试探求S_△MON与S_△AOB之间的关系。
②当S_△MON=S_△AOB时，试判断直线AD与⊙M的位置关系，并说明理由。

已知△ABC，∠ACB=90º，AC=BC，点E、F在AB上，∠ECF=45º，设△ABC的面积为S，说明AF·BE=2S的理由。

已知：把Rt△ABC和Rt△DEF按如图甲摆放（点C与点E重合），点B、C（E）、F在同一条直线上．∠BAC = ∠DEF = 90°，∠ABC = 45°，BC =" 9" cm，DE =" 6" cm，EF =" 8" cm．
如图乙，△DEF从图甲的位置出发，以1 cm/s的速度沿CB向△ABC匀速移动，在△DEF移动的同时，点P从△DEF的顶点F出发，以3 cm/s的速度沿FD向点D匀速移动．当点P移动到点D时，P点停止移动，△DEF也随之停止移动．DE与AC相交于点Q，连接BQ、PQ，设移动时间为t（s）．解答下列问题：
设三角形BQE的面积为y（cm²），求y与t之间的函数关系式，并写出自变量t的取值范围；
当t为何值时，三角形DPQ为等腰三角形？
是否存在某一时刻t，使P、Q、B三点在同一条直线上？若存在，求出此时t的值；若不存在，说明理由

如图，□ABCD中，AE⊥BD，CF⊥BD，垂足分别为E、F。

写出图中每一对你认为全等的三角形
选择(1)中的任意一对进行证明。

如图，在△ABC中，AB=AC，以AB为直径的⊙O交AC与E，交BC与D．求证：

是的中点；（
△∽△；
。

在直角三角形ABC中，角A=90度，AB=8，AC=6，若动点D从点B出发，沿线段BA运动到点A为止，运动速度为每秒钟2个单位长度，过点D作DE平行于BC交于E，设动点D运动的时间为x秒，AE的长为y。

(1)求y与x之间的函数关系式，并写出自变量x的取值范围
（2）求出△BDE的面积S与x之间的函数关系式；
（3）当x为何值时，△BDE的面积S有最大值，最大值为多少？

如图，在△ABC中，D是BC边上一点，E是AC边上一点，且满足AD=AB，∠ADE=∠C
求证：∠AED=∠ADC，∠DEC=∠B；
求证：AB²=AE·AC

如图（1），已知正方形ABCD在直线MN的上方，BC在直线MN上，E是BC上一点，以AE为边在直线MN的上方作正方形AEFG．

连接GD，求证：△ADG≌△ABE
连接FC，观察并猜测∠FCN的度数，并说明理由；
）如图（2），将图（1）中正方形ABCD改为矩形ABCD，AB=a，BC=b（a、b为常数），E是线段BC上一动点（不含端点B、C），以AE为边在直线MN的上方作矩形AEFG，使顶点G恰好落在射线CD上．判断当点E由B向C运动时，∠FCN的大小是否总保持不变，若∠FCN的大小不变，请用含a、b的代数式表示tan∠FCN的值；若∠FCN的大小发生改变，请举例说明．